Selection SortThe selection sort enhances the bubble sort by making only a single swap for each pass through the rundown. In order to do this, a selection sort searches for the biggest value as it makes a pass and, after finishing the pass, places it in the best possible area. Similarly, as with a bubble sort, after the first pass, the biggest item is in the right place. After the second pass, the following biggest is set up. This procedure proceeds and requires n-1 goes to sort n item since the last item must be set up after the (n-1) th pass. ALGORITHM: SELECTION SORT (A)How Selection Sort works

1st Iteration: Set minimum = 7
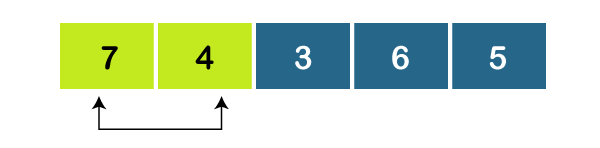
As, a0 > a1, set minimum = 4.
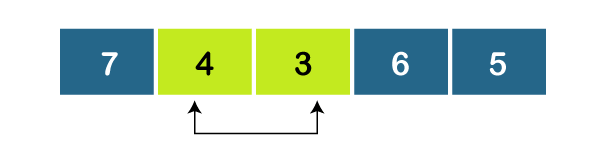
As, a1 > a2, set minimum = 3.
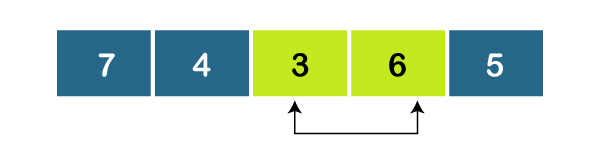
As, a2 < a3, set minimum= 3.
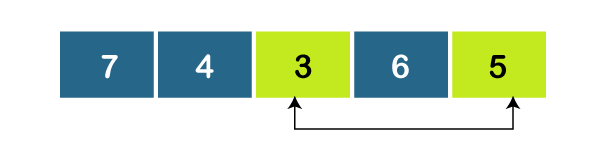
As, a2 < a4, set minimum =3. Since 3 is the smallest element, so we will swap a0 and a2. 
2nd Iteration: Set minimum = 4
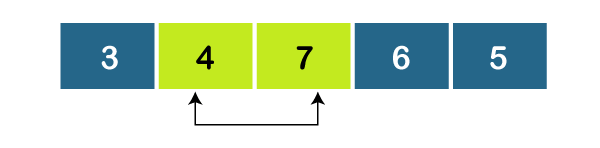
As, a1 < a2, set minimum = 4.

As, A[1] < A[3], set minimum = 4.
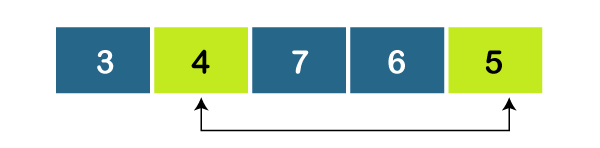
Again, a1 < a4, set minimum = 4. Since the minimum is already placed in the correct position, so there will be no swapping. 
3rd Iteration: Set minimum = 7
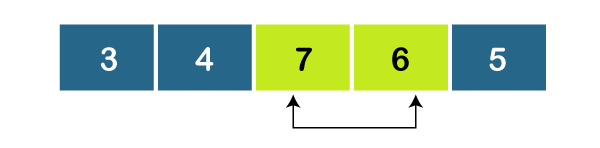
As, a2 > a3, set minimum = 6.

As, a3 > a4, set minimum = 5. Since 5 is the smallest element among the leftover unsorted elements, so we will swap 7 and 5. 
4th Iteration: Set minimum = 6

As a3 < a4, set minimum = 6. Since the minimum is already placed in the correct position, so there will be no swapping. 
Complexity Analysis of Selection SortInput: Given n input elements. Output: Number of steps incurred to sort a list. Logic: If we are given n elements, then in the first pass, it will do n-1 comparisons; in the second pass, it will do n-2; in the third pass, it will do n-3 and so on. Thus, the total number of comparisons can be found by; 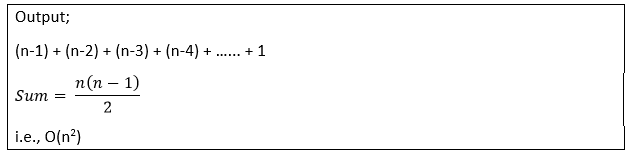
Therefore, the selection sort algorithm encompasses a time complexity of O(n2) and a space complexity of O(1) because it necessitates some extra memory space for temp variable for swapping. Time Complexities:
In the selection sort algorithm, the time complexity is O(n2) in all three cases. This is because, in each step, we are required to find minimum elements so that it can be placed in the correct position. Once we trace the complete array, we will get our minimum element.
Next TopicDAA Insertion Sort
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










