Merge SortMerge sort is yet another sorting algorithm that falls under the category of Divide and Conquer technique. It is one of the best sorting techniques that successfully build a recursive algorithm. Divide and Conquer StrategyIn this technique, we segment a problem into two halves and solve them individually. After finding the solution of each half, we merge them back to represent the solution of the main problem. Suppose we have an array A, such that our main concern will be to sort the subsection, which starts at index p and ends at index r, represented by A[p..r]. Divide If assumed q to be the central point somewhere in between p and r, then we will fragment the subarray A[p..r] into two arrays A[p..q] and A[q+1, r]. Conquer After splitting the arrays into two halves, the next step is to conquer. In this step, we individually sort both of the subarrays A[p..q] and A[q+1, r]. In case if we did not reach the base situation, then we again follow the same procedure, i.e., we further segment these subarrays followed by sorting them separately. Combine As when the base step is acquired by the conquer step, we successfully get our sorted subarrays A[p..q] and A[q+1, r], after which we merge them back to form a new sorted array [p..r]. Merge Sort algorithmThe MergeSort function keeps on splitting an array into two halves until a condition is met where we try to perform MergeSort on a subarray of size 1, i.e., p == r. And then, it combines the individually sorted subarrays into larger arrays until the whole array is merged. Here we called MergeSort(A, 0, length(A)-1) to sort the complete array. As you can see in the image given below, the merge sort algorithm recursively divides the array into halves until the base condition is met, where we are left with only 1 element in the array. And then, the merge function picks up the sorted sub-arrays and merge them back to sort the entire array. The following figure illustrates the dividing (splitting) procedure. 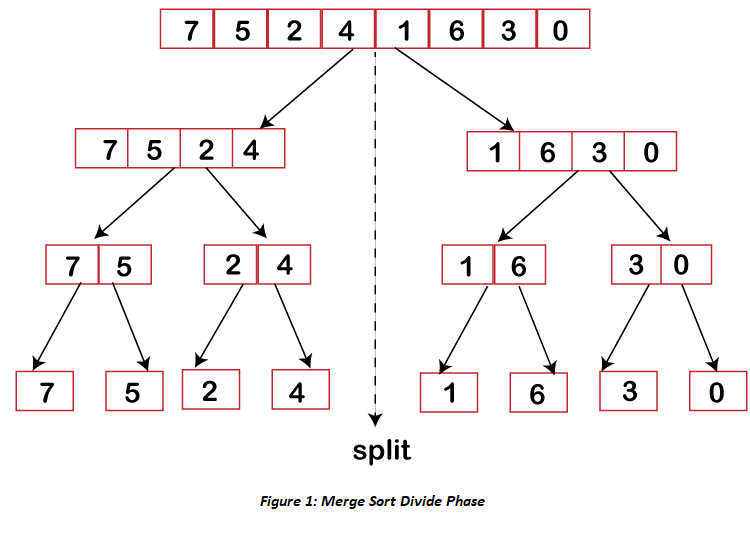
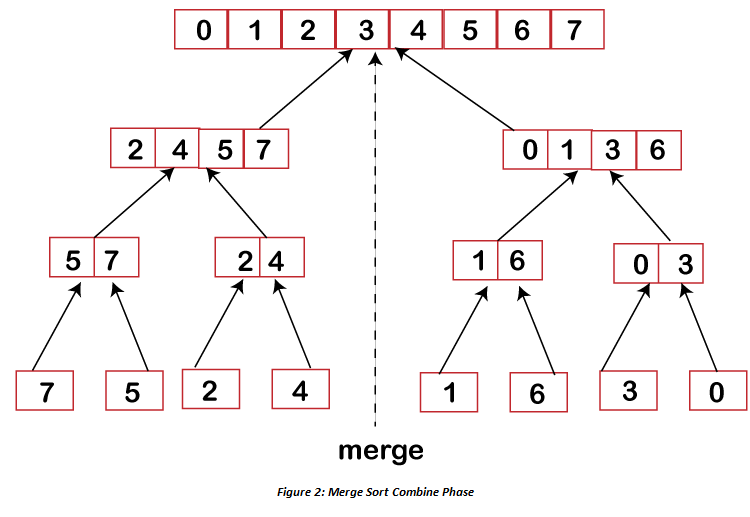
The merge step of Merge SortMainly the recursive algorithm depends on a base case as well as its ability to merge back the results derived from the base cases. Merge sort is no different algorithm, just the fact here the merge step possesses more importance. To any given problem, the merge step is one such solution that combines the two individually sorted lists(arrays) to build one large sorted list(array). The merge sort algorithm upholds three pointers, i.e., one for both of the two arrays and the other one to preserve the final sorted array's current index. Merge( ) Function Explained Step-By-StepConsider the following example of an unsorted array, which we are going to sort with the help of the Merge Sort algorithm. A= (36,25,40,2,7,80,15) Step1: The merge sort algorithm iteratively divides an array into equal halves until we achieve an atomic value. In case if there are an odd number of elements in an array, then one of the halves will have more elements than the other half. Step2: After dividing an array into two subarrays, we will notice that it did not hamper the order of elements as they were in the original array. After now, we will further divide these two arrays into other halves. Step3: Again, we will divide these arrays until we achieve an atomic value, i.e., a value that cannot be further divided. Step4: Next, we will merge them back in the same way as they were broken down. Step5: For each list, we will first compare the element and then combine them to form a new sorted list. Step6: In the next iteration, we will compare the lists of two data values and merge them back into a list of found data values, all placed in a sorted manner. 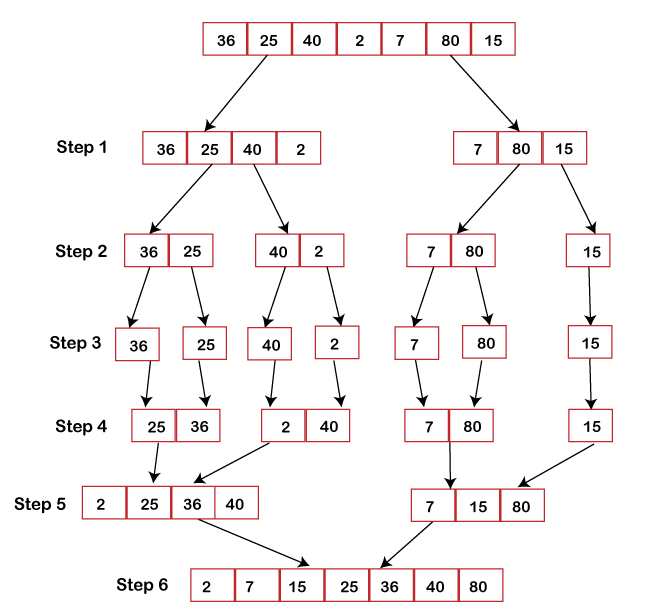
Hence the array is sorted. Analysis of Merge Sort:Let T (n) be the total time taken by the Merge Sort algorithm.
Thus, the relational formula will be 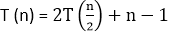
But we ignore '-1' because the element will take some time to be copied in merge lists. So T (n) = 2T Note: Stopping Condition T (1) =0 because at last, there will be only 1 element left that need to be copied, and there will be no comparison.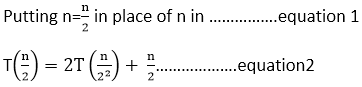
Put 2 equation in 1 equation 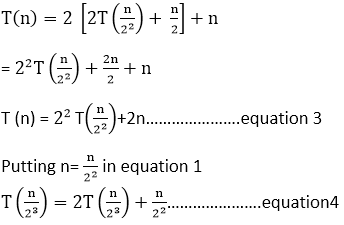
Putting 4 equation in 3 equation 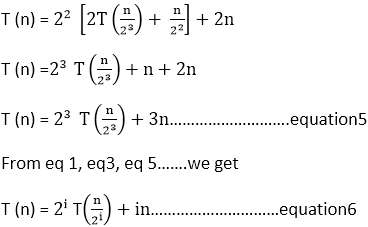
From Stopping Condition: 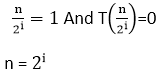
Apply log both sides: log n=log2i From 6 equation 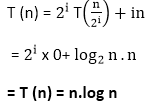
Best Case Complexity: The merge sort algorithm has a best-case time complexity of O(n*log n) for the already sorted array. Average Case Complexity: The average-case time complexity for the merge sort algorithm is O(n*log n), which happens when 2 or more elements are jumbled, i.e., neither in the ascending order nor in the descending order. Worst Case Complexity: The worst-case time complexity is also O(n*log n), which occurs when we sort the descending order of an array into the ascending order. Space Complexity: The space complexity of merge sort is O(n). Merge Sort ApplicationsThe concept of merge sort is applicable in the following areas:
Next TopicTower of Hanoi
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





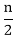 time.
time.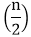 + n...equation 1
+ n...equation 1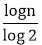 =i
=i




