Greedy Algorithm

The greedy method is one of the strategies like Divide and conquer used to solve the problems. This method is used for solving optimization problems. An optimization problem is a problem that demands either maximum or minimum results. Let's understand through some terms.

The Greedy method is the simplest and straightforward approach. It is not an algorithm, but it is a technique. The main function of this approach is that the decision is taken on the basis of the currently available information. Whatever the current information is present, the decision is made without worrying about the effect of the current decision in future.

This technique is basically used to determine the feasible solution that may or may not be optimal. The feasible solution is a subset that satisfies the given criteria. The optimal solution is the solution which is the best and the most favorable solution in the subset. In the case of feasible, if more than one solution satisfies the given criteria then those solutions will be considered as the feasible, whereas the optimal solution is the best solution among all the solutions.

Characteristics of Greedy method

The following are the characteristics of a greedy method:

• To construct the solution in an optimal way, this algorithm creates two sets where one set contains all the chosen items, and another set contains the rejected items.
• A Greedy algorithm makes good local choices in the hope that the solution should be either feasible or optimal.

Components of Greedy Algorithm

The components that can be used in the greedy algorithm are:

• Candidate set: A solution that is created from the set is known as a candidate set.
• Selection function: This function is used to choose the candidate or subset which can be added in the solution.
• Feasibility function: A function that is used to determine whether the candidate or subset can be used to contribute to the solution or not.
• Objective function: A function is used to assign the value to the solution or the partial solution.
• Solution function: This function is used to intimate whether the complete function has been reached or not.

Applications of Greedy Algorithm

• It is used in finding the shortest path.
• It is used to find the minimum spanning tree using the prim's algorithm or the Kruskal's algorithm.
• It is used in a job sequencing with a deadline.
• This algorithm is also used to solve the fractional knapsack problem.

Pseudo code of Greedy Algorithm

The above is the greedy algorithm. Initially, the solution is assigned with zero value. We pass the array and number of elements in the greedy algorithm. Inside the for loop, we select the element one by one and checks whether the solution is feasible or not. If the solution is feasible, then we perform the union.

Let's understand through an example.

Suppose there is a problem 'P'. I want to travel from A to B shown as below:

P : A → B

The problem is that we have to travel this journey from A to B. There are various solutions to go from A to B. We can go from A to B by walk, car, bike, train, aeroplane, etc. There is a constraint in the journey that we have to travel this journey within 12 hrs. If I go by train or aeroplane then only, I can cover this distance within 12 hrs. There are many solutions to this problem but there are only two solutions that satisfy the constraint.

If we say that we have to cover the journey at the minimum cost. This means that we have to travel this distance as minimum as possible, so this problem is known as a minimization problem. Till now, we have two feasible solutions, i.e., one by train and another one by air. Since travelling by train will lead to the minimum cost so it is an optimal solution. An optimal solution is also the feasible solution, but providing the best result so that solution is the optimal solution with the minimum cost. There would be only one optimal solution.

The problem that requires either minimum or maximum result then that problem is known as an optimization problem. Greedy method is one of the strategies used for solving the optimization problems.

Disadvantages of using Greedy algorithm

Greedy algorithm makes decisions based on the information available at each phase without considering the broader problem. So, there might be a possibility that the greedy solution does not give the best solution for every problem.

It follows the local optimum choice at each stage with a intend of finding the global optimum. Let's understand through an example.

Consider the graph which is given below: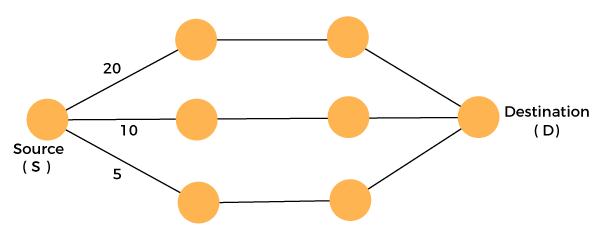

We have to travel from the source to the destination at the minimum cost. Since we have three feasible solutions having cost paths as 10, 20, and 5. 5 is the minimum cost path so it is the optimal solution. This is the local optimum, and in this way, we find the local optimum at each stage in order to calculate the global optimal solution.