Traveling-salesman Problem

In the traveling salesman Problem, a salesman must visits n cities. We can say that salesman wishes to make a tour or Hamiltonian cycle, visiting each city exactly once and finishing at the city he starts from. There is a non-negative cost c (i, j) to travel from the city i to city j. The goal is to find a tour of minimum cost. We assume that every two cities are connected. Such problems are called Traveling-salesman problem (TSP).

We can model the cities as a complete graph of n vertices, where each vertex represents a city.

It can be shown that TSP is NPC.

If we assume the cost function c satisfies the triangle inequality, then we can use the following approximate algorithm.

Triangle inequality

Let u, v, w be any three vertices, we have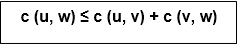

One important observation to develop an approximate solution is if we remove an edge from H*, the tour becomes a spanning tree.

Approx-TSP (G= (V, E)) 
{
  1. Compute a MST T of G;
  2. Select any vertex r is the root of the tree;
  3. Let L be the list of vertices visited in a preorder tree walk of T;
  4. Return the Hamiltonian cycle H that visits the vertices in the order L;
}

Traveling-salesman Problem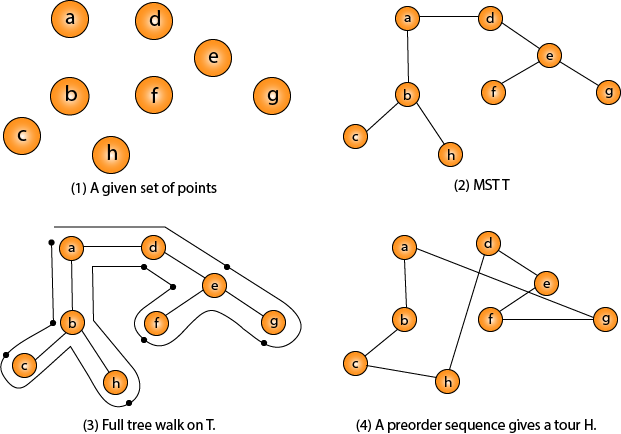

Intuitively, Approx-TSP first makes a full walk of MST T, which visits each edge exactly two times. To create a Hamiltonian cycle from the full walk, it bypasses some vertices (which corresponds to making a shortcut)

Next TopicString Matching

← prev next →