Longest Palindromic SubsequenceBefore knowing about the longest palindromic subsequence, we should about "what is subsequence". A subsequence is a sequence that is achieved from the sequence by removing some of the elements from the sequence without changing the order of the remaining elements. Here we have to find the longest Palindromic Subsequence in the given string. Let's understand through some examples. Example 1: Input string: "a d b b c a" The longest palindromic subsequence is "a b b a". The length of the subsequence is 4. Example 2: Input string: "p q r d r p d" The longest palindromic subsequence is "p r d r p". The length of the subsequence is 5. Example 3: Input string: "p q r r q p" The longest palindromic subsequence is "p q r r q p". The length of the subsequence is 6. In order to solve this problem, we will use the dynamic programming. Here we use the memorization matrix. Suppose the string which is given below: Input string: "a g b d b a". Here, we consider the matrix of same length as that of the string. The length of the string is 6 so we consider the matrix as 6*6. The indices of characters 'a', 'g', 'b', 'd', 'b', 'a' are 0, 1, 2, 3, 4, 5 respectively.
First, we consider the length equal to 1, i.e., l = 1. It means that we consider the single character at a time. If we are considering the single character then the length of the longest palindromic subsequence would also be equal to 1.
Now we consider the length of string as 2. It means that we consider two characters at a time. First, we consider "a g" as a string. Since both the characters are different so the length of the longest palindromic subsequence would be 1 shown as below:
Now we consider another string as "gb". It means that we consider two characters at a time. Since both the characters are different so the length of the longest palindromic subsequence would be 1 shown as below:
Now we consider another string as "bd". It means that we consider two characters at a time. Since both the characters are different so the length of the longest palindromic subsequence would be 1 shown as below:
Now we consider another string as "db". It means that we consider two characters at a time. Since both the characters are different so the length of the longest palindromic subsequence would be 1 shown as below:
Now we consider another string as "ba". It means that we consider two characters at a time. Since both the characters are different so the length of the longest palindromic subsequence would be 1 shown as below:
Consider the length of the string as 3, i.e., "a g b". It means that we consider three characters at a time. Since the first and the last character of a string is different so we consider either "ag" or "gb". The length of "ag" and "gb" is 1 so we put 1 at S[1][2] shown as below:
Consider the string as "g b d". It means that we consider three characters at a time. Since the first and the last character of a string is different so we consider either "gb" or "bd". The length of "gb" and "bd" is 1 so we put 1 at S[1][3] shown as below:
Consider the string as "b d b". It means that we consider three characters at a time. Since the first and the last character of a string is same so the maximum palindromic subsequence would be equal to (2 + 1), i.e., 3. We put 3 at S[1][4] shown as below:
Consider the string as "d b a". It means that we consider three characters at a time. Since the first and the last character of a string is different so we consider either "db" or "ba". The length of "db" and "ba" is 1 so we put 1 at S[1][5] shown as below:
Now we have length l=4. We consider the indices from 0 to 3. Consider the string as "a g b d". It means that we consider four characters at a time. Since the first and the last character of a string is different so we take three characters string either "a g b" or "g b d". The length of both "a g b" and "g b d" is same, i.e., 1 so we put 1 at S[0][3].
Consider the indices from 1 to 4. Consider the string as "g b d b". It means that we consider four characters at a time. Since the first and the last character of a string is different so we take three characters string at a time either "g b d" or "b d b". The length of palindromic subsequence of string "b d b" is maximum, i.e., 3, so we add 3 at S[1][4].
Consider the indices from 2 to 5. Consider the string as "b d b a". It means that we consider four characters at a time. Since the first and the last character of a string is different so consider the three-character string either "b d b" or "d b a". The length of the palindromic subsequence of string "b d b" is maximum, i.e., 3, so we add 3 at S[2][5] shown as below:
Now we have length l = 5. Consider the indices from 0 to 4. Consider the string as "a g b d b". It means that we take five characters at a time. Since the first and the last character of a string is different so we consider the four-character string either as "a g b d" or "g b d b". The length of the palindromic subsequence of string "g b d b" is 3 which is maximum so we add 3 at S[0][4] shown as below:
Consider the indices from 1 to 5. Consider the string as "g b d b a". It means that we take five characters at a time. Since the first and the last character of a string is different so we consider the four-character string either as "g b d b" or "b d b a". Both the strings have the same length, i.e., 3, we add 3 at S[1][5] shown as below:
Now we have length l =6. Consider the indices from 0 to 5. Consider the string as "a g b d b a". It means that we take six characters at a time. Since the first and the last character of a string is same, so the value at S[0][5] would be equal to 2 plus value at S[1][4], i.e. (2+3) equal to 5 shown as below:
As we can observe in the above table that considering string "a g b d b a" produces the length of the palindromic subsequence, i.e., 5. Since the length 5 comes from the string "g b d b" having length 3, the length 3 comes from the string "b d b" having length equal to 3, and the length 3 comes from the string "d" having length 1 shown as below: 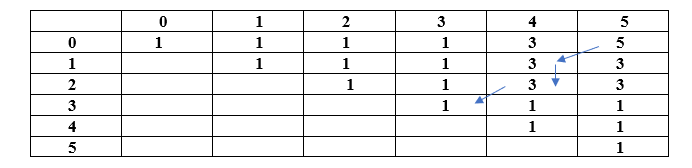
Now we will find the string. Since 5 comes from 3; therefore, the character at 0 and 5 would be included in the string, i.e., 'a' shown as below: S: a a Since 3 comes from the length 3; therefore, the characters at 2 and 4 would be included in the string shown as below: S: a b b a Since the length 3 comes from 1; therefore, the character at 3, i.e., 'd' would be included in the string shown as below: S: a b d b a In this problem, the palindromic subsequence is "a b d b a" which is having the maximum palindromic subsequence (5). Algorithm of palindromic subsequence Implementation in C Output 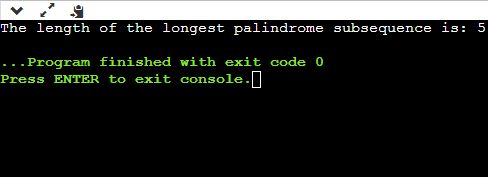
Next TopicLongest Increasing Subsequence
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









