Insertion SortInsertion sort is one of the simplest sorting algorithms for the reason that it sorts a single element at a particular instance. It is not the best sorting algorithm in terms of performance, but it's slightly more efficient than selection sort and bubble sort in practical scenarios. It is an intuitive sorting technique. Let's consider the example of cards to have a better understanding of the logic behind the insertion sort. Suppose we have a set of cards in our hand, such that we want to arrange these cards in ascending order. To sort these cards, we have a number of intuitive ways. One such thing we can do is initially we can hold all of the cards in our left hand, and we can start taking cards one after other from the left hand, followed by building a sorted arrangement in the right hand. Assuming the first card to be already sorted, we will select the next unsorted card. If the unsorted card is found to be greater than the selected card, we will simply place it on the right side, else to the left side. At any stage during this whole process, the left hand will be unsorted, and the right hand will be sorted. In the same way, we will sort the rest of the unsorted cards by placing them in the correct position. At each iteration, the insertion algorithm places an unsorted element at its right place. ALGORITHM: INSERTION SORT (A)How Insertion Sort Works1. We will start by assuming the very first element of the array is already sorted. Inside the key, we will store the second element. Next, we will compare our first element with the key, such that if the key is found to be smaller than the first element, we will interchange their indexes or place the key at the first index. After doing this, we will notice that the first two elements are sorted. 2. Now, we will move on to the third element and compare it with the left-hand side elements. If it is the smallest element, then we will place the third element at the first index. Else if it is greater than the first element and smaller than the second element, then we will interchange its position with the third element and place it after the first element. After doing this, we will have our first three elements in a sorted manner. 3. Similarly, we will sort the rest of the elements and place them in their correct position. Consider the following example of an unsorted array that we will sort with the help of the Insertion Sort algorithm. A = (41, 22, 63, 14, 55, 36) Initially, 
1st Iteration: Set key = 22 Compare a1 with a0 
Since a0 > a1, swap both of them. 
2nd Iteration: Set key = 63 Compare a2 with a1 and a0 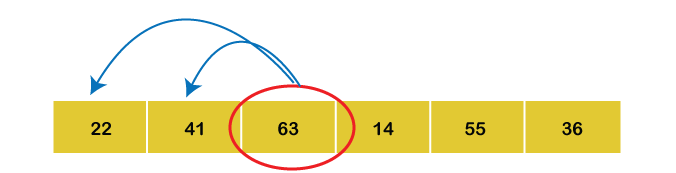
Since a2 > a1 > a0, keep the array as it is. 
3rd Iteration: Set key = 14 Compare a3 with a2, a1 and a0 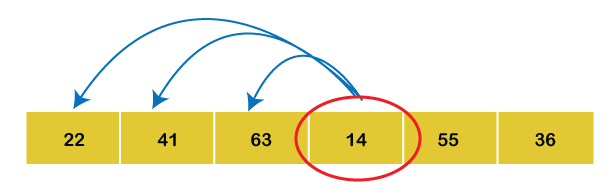
Since a3 is the smallest among all the elements on the left-hand side, place a3 at the beginning of the array. 
4th Iteration: Set key = 55 Compare a4 with a3, a2, a1 and a0. 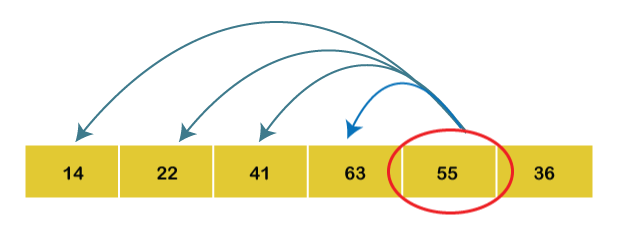
As a4 < a3, swap both of them. 
5th Iteration: Set key = 36 Compare a5 with a4, a3, a2, a1 and a0. 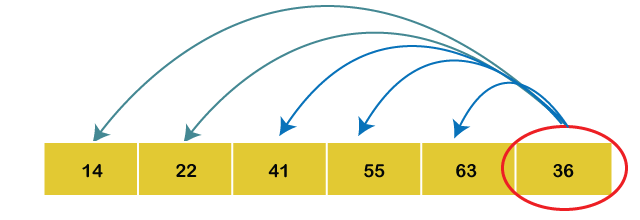
Since a5 < a2, so we will place the elements in their correct positions. 
Hence the array is arranged in ascending order, so no more swapping is required. Complexity Analysis of Insertion SortInput: Given n input elements. Output: Number of steps incurred to sort a list. Logic: If we are given n elements, then in the first pass, it will make n-1 comparisons; in the second pass, it will do n-2; in the third pass, it will do n-3 and so on. Thus, the total number of comparisons can be found by; Output; (n-1) + (n-2) + (n-3) + (n-4) + ...... + 1 Sum= Therefore, the insertion sort algorithm encompasses a time complexity of O(n2) and a space complexity of O(1) because it necessitates some extra memory space for a key variable to perform swaps. Time Complexities:
The insertion sort algorithm is highly recommended, especially when a few elements are left for sorting or in case the array encompasses few elements. Space ComplexityThe insertion sort encompasses a space complexity of O(1) due to the usage of an extra variable key. Insertion Sort ApplicationsThe insertion sort algorithm is used in the following cases:
Advantages of Insertion Sort
Next TopicDivide and Conquer Introduction
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










