Tabulation vs Memoization

There are two ways of implementing the dynamic programming, or we can say that there are two ways of storing the solution of sub-problem so that it can be reused.

Tabulation
Memoization

Let's understand each approach one by one in brief.

What is tabulation?

Tabulation is a technique that is used to implement the DP algorithms. It is also known as a bottom-up approach. It starts from solving the lowest level sub-problem. The solution to the lowest level sub-problem will help to solve next level sub-problem, and so forth. We solve all the sub-problems iteratively until we solve all the sub-problems. This approach saves the time when a sub-problem needs a solution of the sub-problem that has been solved before.

Let's understand the tabulation through an example.

Consider an example of the Fibonacci series.

Suppose we need to calculate the F(5) term.

In order to calculate the F(5) term, some sub-problems appear more than once. For example, F(3) sub-problem occurs twice, and F(4) sub-problem occurs four times.

Despite of calculating the same sub-problem, again and again, we can store the result of a sub-problem once and can use the result whenever required.

Let's look at the code without storing the result.

FIBONACCI(n)
  if n==0
    return 0
  if n==1
    return 1
  return FIBONACCI(n-1) + FIBONACCI(n-2)

In the above code, we are simply calculating the Fibonacci series without storing results. The values of F(0) and F(1) are 0 and 1, respectively. The value of the nth term is calculated using the Fibonacci(n-1)+Fibonacci(n-2).

F = [] //new array
FIBONACCI(n)
  if F[n] == null
    if n==0
      F[n] = 0
    else if n==1
      F[n] = 1
    else
      F[n] = FIBONACCI(n-1) + FIBONACCI(n-2)
  return F[n]

The above code computes the Fibonacci series by storing the results of all the sub-problems. We use the condition F[n] == null to determine whether the result is present or not in the array.

What is Memoization?

Memoization is a technique that is used to implement the DP algorithms. Memoization is also known as a top-down approach. It starts from solving the highest-level sub-problems. Initially, it solves the highest-level subproblem and then solve the next sub-problem recursively and the next. Suppose there are two sub-problems, i.e., sub-problem A and sub-problem B. When sub-problem B is called recursively, then it can use the solution of sub-problem A, which has already been used. Since A and all the sub-problems are memoized, it avoids solving the entire recursion tree generated by B and saves computation time.

Let's understand the memoization through an example of the Fibonacci sequence.

The sequence of numbers in which number is the sum of two preceding numbers. The Fibonacci sequence is 0, 1, 1, 2, 3, 5, 8, 13, etc.

The condition for calculating the Fibonacci sequence is given below:

F(n) = 0 if n = 0

1 if n = 1

F(n-1) + f(n-2) if n>1

Program with recursive solution

def fib(n)
 if(n==0) or (n==1)
return n
else:
result = fib(n-1) + fib(n-2)
return result

The time complexity to find the recursive solution is O(2ⁿ).

Program with memoization

def fib(n, memo):
  if memo[n] is not None:
   return memo[n]
 if n==0 or n==1
   return n
else:
result = fib(n-1, memo)  + fib(n-2, memo)
memo[n] = result
return result
def fib_memo(n):
memo = [None] * (n+1)
 return fib(n, memo)

The above code is used for memoization. Memoization is a technique used for storing all the solved sub-problems so that we do not need to recalculate the solutions of the already solved sub-problems, and it also reduces the time complexity.

Let's understand the differences between the tabulation and memoization.

1. Tabulation: Tabulation is a technique used for solving the sub-problem recursively. The below code shows the working of the tabulation:

int fib(int n)
{
    if(n<=1)
    return n;
  else
return fib(n-2) + fib(n-1)
} 

Suppose we want to calculate the fibonacci sequence of f(5). The Fibonacci sequence of f(5) is 0, 1, 1, 2, 3, 5. There is a total 15 calls to be used to calculate f(15).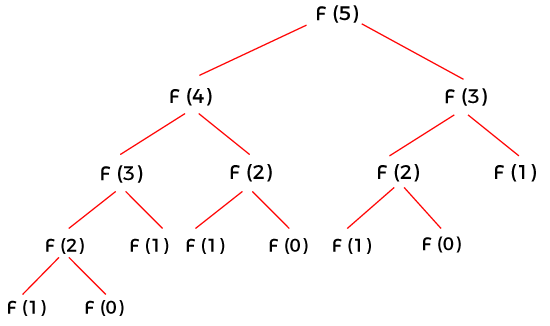

Memoization: Memoization is a technique used for solving the sub-problem non-recursively.

int fib(int n)
{
    if(n<=1)
    return n;
    f[0] = 0, f[1] = 1;
    for i=2 to n
    {
       f[i] = f[i-2] + f[i-1]
    }
   return f[n];
} 

The above code takes a time complexity of O(2ⁿ). This time complexity is non-linear. To reduce this time complexity, we can use the technique of memoization. This technique reduces the number of calls, and it reduces the time complexity.

2. State transition

The tabulation is also known as a bottom-up approach. It starts from the base state, which is 0. Once the base state 0 is solved, it moves to state 1. State 1 requires the solution of the base state 0. Once state 1 is solved, we move to state 2. The state 2 requires the solution of state 1. This process will continue till we reach the n state. The 'n' state is a destination state, and it is also known as an up state. This is known as a state transition relationship.

The memoization is also known as a top-down approach. It starts from the topmost state, i.e., n. The 'n' state requires the solution of the 'n-1' state but the 'n-1' state is not yet solved. The 'n-1' state requires the solution of the 'n-2' state in order to solve its state, but 'n-2' state is not yet solved. It will further ask until it reaches the base state. It will recursive calls such as f(n), f(n-1), f(n-2), ...,0, 1. So, here we have started from the topmost state, and recursively we reached the base state.

Let's understand this concept through an example.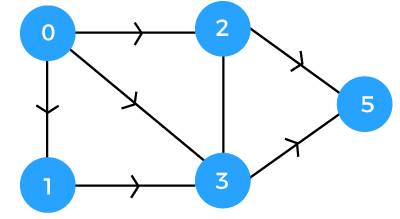

In the above figure, '0' is the source vertex while 5 is the destination vertex. To reach vertex 5, we can either reach from 2 or 3. The decision would be based on the distance between the vertices. Let's assume that the distance between the vertices (0,2) is 1 and (0,3) is 2. If we consider vertex 2, then the distance from the vertex 0 to 5 is (1+1) =2. If we consider vertex 3, then the distance from the vertex 0 to 5 is (2+1) = 3. The minimum distance is 2 so we will consider vertex 2 to reach vertex 5.

Differences between the tabulation and memorization

The following is the list of differences between tabulation and memoization:

Tabulation	Memoization
In tabulation, the state transition is difficult to create.	State transition relation is easy to create.
Code becomes difficult when lots of conditions are needed.	Code is not complicated and it's not difficult to create.
It is fast as the result of the previously solved sub-problems can be directly accessed from the table.	It is slow because lots of recursive calls and return statements are required.
In a tabulated version, all the entries must be filled one by one.	In a memoized version, entries in the table are filled on demand.