Open Addressing TechniquesThree techniques are commonly used to compute the probe sequence required for open addressing:
1. Linear Probing:It is a Scheme in Computer Programming for resolving collision in hash tables. Suppose a new record R with key k is to be added to the memory table T but that the memory locations with the hash address H (k). H is already filled. Our natural key to resolve the collision is to crossing R to the first available location following T (h). We assume that the table T with m location is circular, so that T [i] comes after T [m]. The above collision resolution is called "Linear Probing". Linear probing is simple to implement, but it suffers from an issue known as primary clustering. Long runs of occupied slots build up, increasing the average search time. Clusters arise because an empty slot proceeded by i full slots gets filled next with probability (i + 1)/m. Long runs of occupied slots tend to get longer, and the average search time increases. Given an ordinary hash function h': U {0, 1...m-1}, the method of linear probing uses the hash function. Where 'm' is the size of hash table and h' (k) = k mod m. for i=0, 1....m-1. Given key k, the first slot is T [h' (k)]. We next slot T [h' (k) +1] and so on up to the slot T [m-1]. Then we wrap around to slots T [0], T [1]....until finally slot T [h' (k)-1]. Since the initial probe position dispose of the entire probe sequence, only m distinct probe sequences are used with linear probing. Example: Consider inserting the keys 24, 36, 58,65,62,86 into a hash table of size m=11 using linear probing, consider the primary hash function is h' (k) = k mod m. Solution: Initial state of hash table 
Insert 24. We know h (k, i) = [h' (k) + i] mod m Now h (24, 0) = [24 mod 11 + 0] mod 11 = (2+0) mod 11 = 2 mod 11 = 2 Since T [2] is free, insert key 24 at this place. Insert 36. Now h (36, 0) = [36 mod 11 + 0] mod 11 = [3+0] mod 11 = 3 Since T [3] is free, insert key 36 at this place. Insert 58. Now h (58, 0) = [58 mod 11 +0] mod 11 = [3+0] mod 11 =3 Since T [3] is not free, so the next sequence is h (58, 1) = [58 mod 11 +1] mod 11 = [3+1] mod 11= 4 mod 11=4 T [4] is free; Insert key 58 at this place. Insert 65. Now h (65, 0) = [65 mod 11 +0] mod 11 = (10 +0) mod 11= 10 T [10] is free. Insert key 65 at this place. Insert 62. Now h (62, 0) = [62 mod 11 +0] mod 11 = [7 + 0] mod 11 = 7 T [7] is free. Insert key 62 at this place. Insert 86. Now h (86, 0) = [86 mod 11 + 0] mod 11 = [9 + 0] mod 11 = 9 T [9] is free. Insert key 86 at this place. Thus, 
2. Quadratic Probing:Suppose a record R with key k has the hash address H (k) = h then instead of searching the location with addresses h, h+1, and h+ 2...We linearly search the locations with addresses h, h+1, h+4, h+9...h+i2 Quadratic Probing uses a hash function of the form h (k,i) = (h' (k) + c1i + c2i2) mod m Where (as in linear probing) h' is an auxiliary hash function c1 and c2 ≠0 are auxiliary constants and i=0, 1...m-1. The initial position is T [h' (k)]; later position probed is offset by the amount that depend in a quadratic manner on the probe number i. Example: Consider inserting the keys 74, 28, 36,58,21,64 into a hash table of size m =11 using quadratic probing with c1=1 and c2=3. Further consider that the primary hash function is h' (k) = k mod m. Solution: For Quadratic Probing, we have h (k, i) = [k mod m +c1i +c2 i2) mod m 
This is the initial state of hash table
Here c1= 1 and c2=3
h (k, i) = [k mod m + i + 3i2 ] mod m
Insert 74.
h (74,0)= (74 mod 11+0+3x0) mod 11
= (8 +0+0) mod 11 = 8
T [8] is free; insert the key 74 at this place.
Insert 28.
h (28, 0) = (28 mod 11 + 0 + 3 x 0) mod 11
= (6 +0 + 0) mod 11 = 6.
T [6] is free; insert key 28 at this place.
Insert 36.
h (36, 0) = (36 mod 11 + 0 + 3 x 0) mod 11
= (3 + 0+0) mod 11=3
T [3] is free; insert key 36 at this place.
Insert 58.
h (58, 0) = (58 mod 11 + 0 + 3 x 0) mod 11
= (3 + 0 + 0) mod 11 = 3
T [3] is not free, so next probe sequence is computed as
h (59, 1) = (58 mod 11 + 1 + 3 x12) mod 11
= (3 + 1 + 3) mod 11
=7 mod 11= 7
T [7] is free; insert key 58 at this place.
Insert 21.
h (21, 0) = (21 mod 11 + 0 + 3 x 0)
= (10 + 0) mod 11 = 10
T [10] is free; insert key 21 at this place.
Insert 64.
h (64, 0) = (64 mod 11 + 0 + 3 x 0)
= (9 + 0+ 0) mod 11 = 9.
T [9] is free; insert key 64 at this place.
Thus, after inserting all keys, the hash table is 
3. Double Hashing:Double Hashing is one of the best techniques available for open addressing because the permutations produced have many of the characteristics of randomly chosen permutations. Double hashing uses a hash function of the form h (k, i) = (h1(k) + i h2 (k)) mod m Where h1 and h2 are auxiliary hash functions and m is the size of the hash table. h1 (k) = k mod m or h2 (k) = k mod m'. Here m' is slightly less than m (say m-1 or m-2). Example: Consider inserting the keys 76, 26, 37,59,21,65 into a hash table of size m = 11 using double hashing. Consider that the auxiliary hash functions are h1 (k)=k mod 11 and h2(k) = k mod 9. Solution: Initial state of Hash table is 
1. Insert 76.
h1(76) = 76 mod 11 = 10
h2(76) = 76 mod 9 = 4
h (76, 0) = (10 + 0 x 4) mod 11
= 10 mod 11 = 10
T [10] is free, so insert key 76 at this place.
2. Insert 26.
h1(26) = 26 mod 11 = 4
h2(26) = 26 mod 9 = 8
h (26, 0) = (4 + 0 x 8) mod 11
= 4 mod 11 = 4
T [4] is free, so insert key 26 at this place.
3. Insert 37.
h1(37) = 37 mod 11 = 4
h2(37) = 37 mod 9 = 1
h (37, 0) = (4 + 0 x 1) mod 11 = 4 mod 11 = 4
T [4] is not free, the next probe sequence is
h (37, 1) = (4 + 1 x 1) mod 11 = 5 mod 11 = 5
T [5] is free, so insert key 37 at this place.
4. Insert 59.
h1(59) = 59 mod 11 = 4
h2(59) = 59 mod 9 = 5
h (59, 0) = (4 + 0 x 5) mod 11 = 4 mod 11 = 4
Since, T [4] is not free, the next probe sequence is
h (59, 1) = (4 + 1 x 5) mod 11 = 9 mod 11 = 9
T [9] is free, so insert key 59 at this place.
5. Insert 21.
h1(21) = 21 mod 11 = 10
h2(21) = 21 mod 9 = 3
h (21, 0) = (10 + 0 x 3) mod 11 = 10 mod 11 = 10
T [10] is not free, the next probe sequence is
h (21, 1) = (10 + 1 x 3) mod 11 = 13 mod 11 = 2
T [2] is free, so insert key 21 at this place.
6. Insert 65.
h1(65) = 65 mod 11 = 10
h2(65) = 65 mod 9 = 2
h (65, 0) = (10 + 0 x 2) mod 11 = 10 mod 11 = 10
T [10] is not free, the next probe sequence is
h (65, 1) = (10 + 1 x 2) mod 11 = 12 mod 11 = 1
T [1] is free, so insert key 65 at this place.
Thus, after insertion of all keys the final hash table is
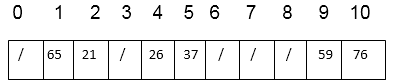
Next TopicHash Function
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










