Prim's Algorithm

It is a greedy algorithm. It starts with an empty spanning tree. The idea is to maintain two sets of vertices:

• Contain vertices already included in MST.
• Contain vertices not yet included.

At every step, it considers all the edges and picks the minimum weight edge. After picking the edge, it moves the other endpoint of edge to set containing MST.

Steps for finding MST using Prim's Algorithm:

1. Create MST set that keeps track of vertices already included in MST.
2. Assign key values to all vertices in the input graph. Initialize all key values as INFINITE (∞). Assign key values like 0 for the first vertex so that it is picked first.
3. While MST set doesn't include all vertices.
   1. Pick vertex u which is not is MST set and has minimum key value. Include 'u'to MST set.
   2. Update the key value of all adjacent vertices of u. To update, iterate through all adjacent vertices. For every adjacent vertex v, if the weight of edge u.v less than the previous key value of v, update key value as a weight of u.v.

MST-PRIM (G, w, r)
 1. for each u ∈ V [G]
 2. do key [u] ← ∞
 3. π [u] ← NIL
 4. key [r] ← 0
 5. Q ← V [G]
 6. While Q ? ∅
 7. do u ← EXTRACT - MIN (Q)
 8. for each v ∈ Adj [u]
 9. do if v ∈ Q and w (u, v) < key [v]
 10. then π [v] ← u
 11. key [v] ← w (u, v)

Example: Generate minimum cost spanning tree for the following graph using Prim's algorithm.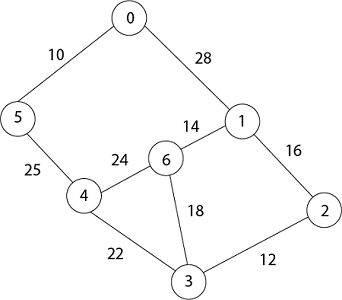

Solution: In Prim's algorithm, first we initialize the priority Queue Q. to contain all the vertices and the key of each vertex to ∞ except for the root, whose key is set to 0. Suppose 0 vertex is the root, i.e., r. By EXTRACT - MIN (Q) procure, now u = r and Adj [u] = {5, 1}.

Removing u from set Q and adds it to set V - Q of vertices in the tree. Now, update the key and π fields of every vertex v adjacent to u but not in a tree.

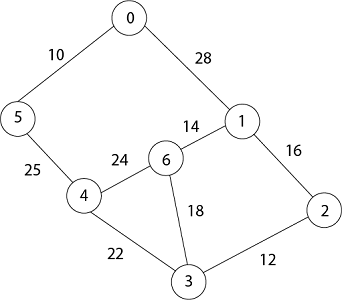
Now by EXTRACT_MIN (Q) Removes 5 because key [5] = 10 which is minimum so u = 5.

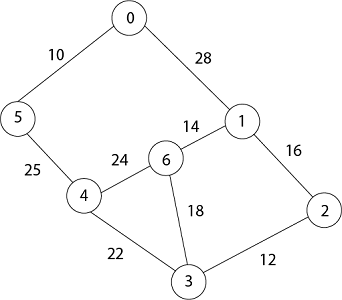
Now remove 4 because key [4] = 25 which is minimum, so u =4

Update key value of key [3] as 22 and key [6] as 24.

And the parent of 3, 6 as 4.

Now remove 3 because key [3] = 22 is minimum so u =3.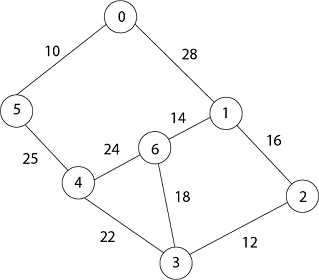

Now in Q, key [2] = 12, key [6] = 18, key [1] = 28 and parent of 2 and 6 is 3.

Now by EXTRACT_MIN (Q) Removes 2, because key [2] = 12 is minimum.

So update key value of key [1] as 16 and its parent as 2.

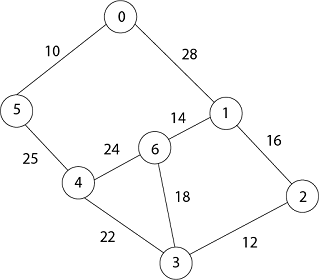
Now by EXTRACT_MIN (Q) Removes 1 because key [1] = 16 is minimum.

Update key value of 6 as 14 and its parent as 1.

Now all the vertices have been spanned, Using above the table we get Minimum Spanning Tree.

Thus the final spanning Tree is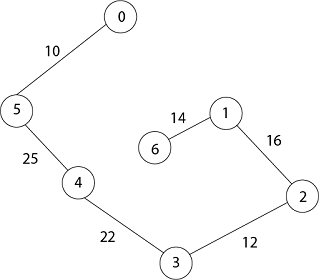

Total Cost = 10 + 25 + 22 + 12 + 16 + 14 = 99