Divide and Conquer Introduction

Divide and Conquer is an algorithmic pattern. In algorithmic methods, the design is to take a dispute on a huge input, break the input into minor pieces, decide the problem on each of the small pieces, and then merge the piecewise solutions into a global solution. This mechanism of solving the problem is called the Divide & Conquer Strategy.

Divide and Conquer algorithm consists of a dispute using the following three steps.

1. Divide the original problem into a set of subproblems.
2. Conquer: Solve every subproblem individually, recursively.
3. Combine: Put together the solutions of the subproblems to get the solution to the whole problem.

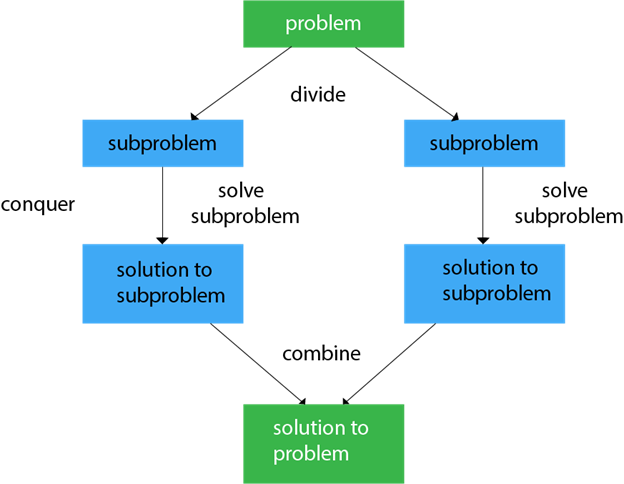
Generally, we can follow the divide-and-conquer approach in a three-step process.

Examples: The specific computer algorithms are based on the Divide & Conquer approach:

1. Maximum and Minimum Problem
2. Binary Search
3. Sorting (merge sort, quick sort)
4. Tower of Hanoi.

Fundamental of Divide & Conquer Strategy:

There are two fundamental of Divide & Conquer Strategy:

1. Relational Formula
2. Stopping Condition

1. Relational Formula: It is the formula that we generate from the given technique. After generation of Formula we apply D&C Strategy, i.e. we break the problem recursively & solve the broken subproblems.

2. Stopping Condition: When we break the problem using Divide & Conquer Strategy, then we need to know that for how much time, we need to apply divide & Conquer. So the condition where the need to stop our recursion steps of D&C is called as Stopping Condition.

Applications of Divide and Conquer Approach:

Following algorithms are based on the concept of the Divide and Conquer Technique:

1. Binary Search: The binary search algorithm is a searching algorithm, which is also called a half-interval search or logarithmic search. It works by comparing the target value with the middle element existing in a sorted array. After making the comparison, if the value differs, then the half that cannot contain the target will eventually eliminate, followed by continuing the search on the other half. We will again consider the middle element and compare it with the target value. The process keeps on repeating until the target value is met. If we found the other half to be empty after ending the search, then it can be concluded that the target is not present in the array.
2. Quicksort: It is the most efficient sorting algorithm, which is also known as partition-exchange sort. It starts by selecting a pivot value from an array followed by dividing the rest of the array elements into two sub-arrays. The partition is made by comparing each of the elements with the pivot value. It compares whether the element holds a greater value or lesser value than the pivot and then sort the arrays recursively.
3. Merge Sort: It is a sorting algorithm that sorts an array by making comparisons. It starts by dividing an array into sub-array and then recursively sorts each of them. After the sorting is done, it merges them back.
4. Closest Pair of Points: It is a problem of computational geometry. This algorithm emphasizes finding out the closest pair of points in a metric space, given n points, such that the distance between the pair of points should be minimal.
5. Strassen's Algorithm: It is an algorithm for matrix multiplication, which is named after Volker Strassen. It has proven to be much faster than the traditional algorithm when works on large matrices.
6. Cooley-Tukey Fast Fourier Transform (FFT) algorithm: The Fast Fourier Transform algorithm is named after J. W. Cooley and John Turkey. It follows the Divide and Conquer Approach and imposes a complexity of O(nlogn).
7. Karatsuba algorithm for fast multiplication: It is one of the fastest multiplication algorithms of the traditional time, invented by Anatoly Karatsuba in late 1960 and got published in 1962. It multiplies two n-digit numbers in such a way by reducing it to at most single-digit.

Advantages of Divide and Conquer

• Divide and Conquer tend to successfully solve one of the biggest problems, such as the Tower of Hanoi, a mathematical puzzle. It is challenging to solve complicated problems for which you have no basic idea, but with the help of the divide and conquer approach, it has lessened the effort as it works on dividing the main problem into two halves and then solve them recursively. This algorithm is much faster than other algorithms.
• It efficiently uses cache memory without occupying much space because it solves simple subproblems within the cache memory instead of accessing the slower main memory.
• It is more proficient than that of its counterpart Brute Force technique.
• Since these algorithms inhibit parallelism, it does not involve any modification and is handled by systems incorporating parallel processing.

Disadvantages of Divide and Conquer

• Since most of its algorithms are designed by incorporating recursion, so it necessitates high memory management.
• An explicit stack may overuse the space.
• It may even crash the system if the recursion is performed rigorously greater than the stack present in the CPU.