Huffman Coding Algorithm

Data may be compressed using the Huffman Coding technique to become smaller without losing any of its information. After David Huffman, who created it in the beginning? Data that contains frequently repeated characters is typically compressed using Huffman coding.

A well-known Greedy algorithm is Huffman Coding. The size of code allocated to a character relies on the frequency of the character, which is why it is referred to be a greedy algorithm. The short-length variable code is assigned to the character with the highest frequency, and vice versa for characters with lower frequencies. It employs a variable-length encoding, which means that it gives each character in the provided data stream a different variable-length code.

Prefix Rule

Essentially, this rule states that the code that is allocated to a character shall not be another code's prefix. If this rule is broken, various ambiguities may appear when decoding the Huffman tree that has been created.

Let's look at an illustration of this rule to better comprehend it: For each character, a code is provided, such as:

    a - 0
    b - 1
    c - 01

Assuming that the produced bit stream is 001, the code may be expressed as follows when decoded:

    0 0 1 = aab
    0 01  = ac

What is the Huffman Coding process?

The Huffman Code is obtained for each distinct character in primarily two steps:

Create a Huffman Tree first using only the unique characters in the data stream provided.
Second, we must proceed through the constructed Huffman Tree, assign codes to the characters, and then use those codes to decode the provided text.

Steps to Take in Huffman Coding

The steps used to construct the Huffman tree using the characters provided

Input:
string str = "abbcdbccdaabbeeebeab"

If Huffman Coding is employed in this case for data compression, the following information must be determined for decoding:

For each character, the Huffman Code
Huffman-encoded message length (in bits), average code length
Utilizing the formulas covered below, the final two of them are discovered.

How Can a Huffman Tree Be Constructed from Input Characters?

The frequency of each character in the provided string must first be determined.

Character	Frequency
a	4
b	7
c	3
d	2
e	4

Sort the characters by frequency, ascending. These are kept in a Q/min-heap priority queue.
For each distinct character and its frequency in the data stream, create a leaf node.
Remove the two nodes with the two lowest frequencies from the nodes, and the new root of the tree is created using the sum of these frequencies.
- Make the first extracted node its left child and the second extracted node its right child while extracting the nodes with the lowest frequency from the min-heap.
- To the min-heap, add this node.
- Since the left side of the root should always contain the minimum frequency.
Repeat steps 3 and 4 until there is only one node left on the heap, or all characters are represented by nodes in the tree. The tree is finished when just the root node remains.

Examples of Huffman Coding

Let's use an illustration to explain the algorithm:

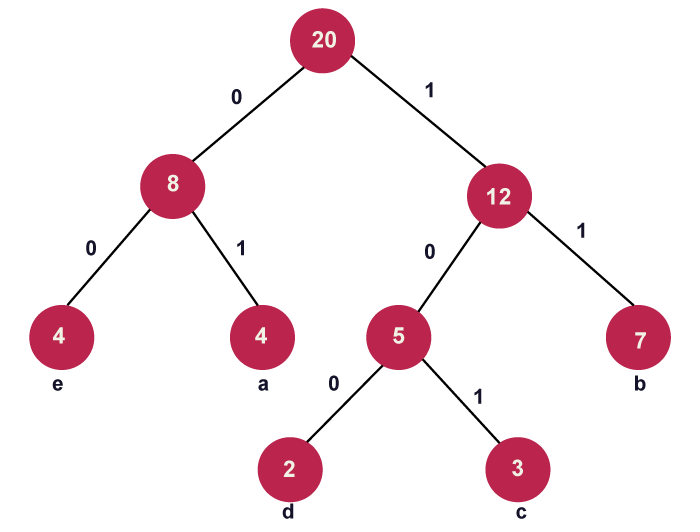
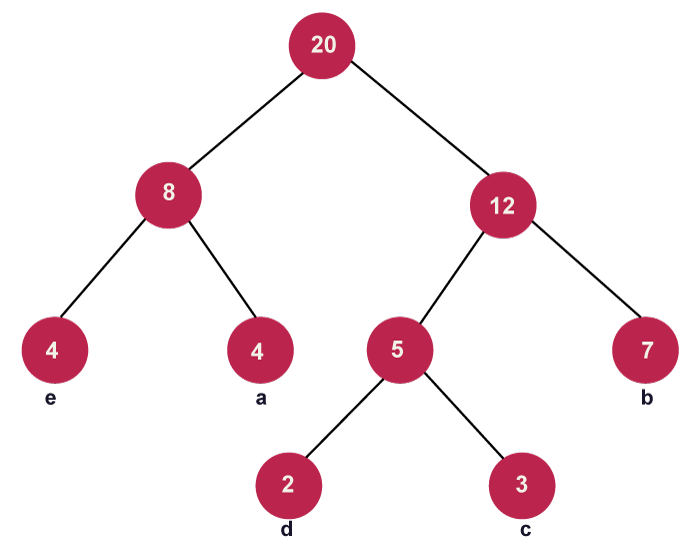
Algorithm for Huffman Coding

Step 1: Build a min-heap in which each node represents the root of a tree with a single node and holds 5 (the number of unique characters from the provided stream of data).

Step 2: Obtain two minimum frequency nodes from the min heap in step two. Add a third internal node, frequency 2 + 3 = 5, which is created by joining the two extracted nodes.

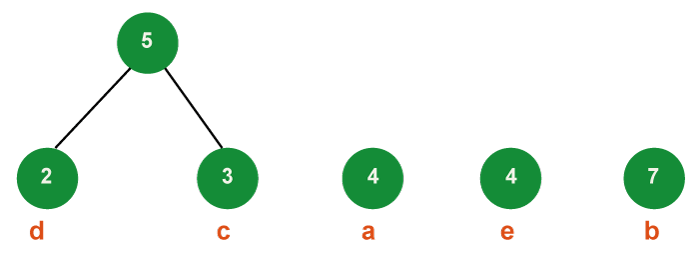
Now, there are 4 nodes in the min-heap, 3 of which are the roots of trees with a single element each, and 1 of which is the root of a tree with two elements.

Step 3: Get the two minimum frequency nodes from the heap in a similar manner in step three. Additionally, add a new internal node formed by joining the two extracted nodes; its frequency in the tree should be 4 + 4 = 8.

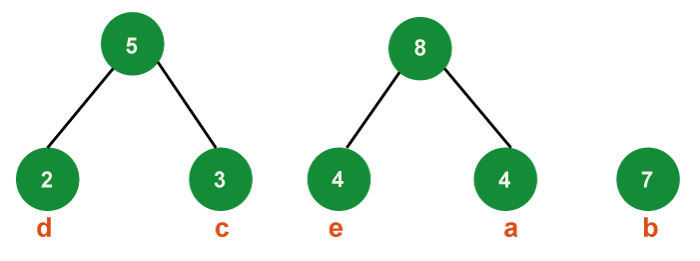
Now that the minimum heap has three nodes, one node serves as the root of trees with a single element and two heap nodes serve as the root of trees with multiple nodes.

Step 4: Get the two minimum frequency nodes in step four. Additionally, add a new internal node formed by joining the two extracted nodes; its frequency in the tree should be 5 + 7 = 12.

When creating a Huffman tree, we must ensure that the minimum value is always on the left side and that the second value is always on the right side. Currently, the image below shows the tree that has formed:

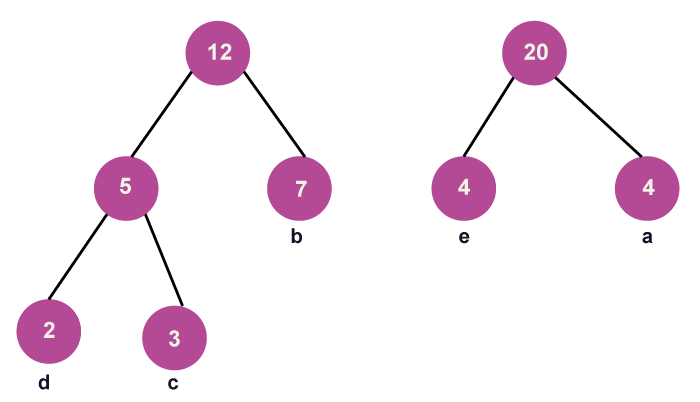
Step 5: Get the following two minimum frequency nodes in step 5. Additionally, add a new internal node formed by joining the two extracted nodes; its frequency in the tree should be 12 + 8 = 20.

Continue until all of the distinct characters have been added to the tree. The Huffman tree created for the specified cast of characters is shown in the above image.

Now, for each non-leaf node, assign 0 to the left edge and 1 to the right edge to create the code for each letter.

Rules to follow for determining edge weights:

We should give the right edges weight 1 if you give the left edges weight 0.
If the left edges are given weight 1, the right edges must be given weight 0.
Any of the two aforementioned conventions may be used.
However, follow the same protocol when decoding the tree as well.

Following the weighting, the modified tree is displayed as follows:

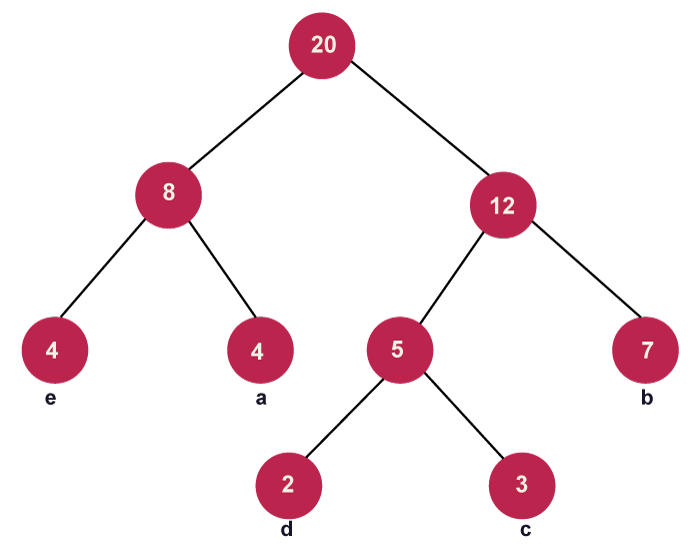
Understanding the Code

We must go through the Huffman tree until we reach the leaf node, where the element is present, in order to decode the Huffman code for each character from the resulting Huffman tree.
The weights across the nodes must be recorded during traversal and allocated to the items located at the specific leaf node.
The following example will help to further illustrate what we mean:
To obtain the code for each character in the picture above, we must walk the entire tree (until all leaf nodes are covered).
As a result, the tree that has been created is used to decode the codes for each node. Below is a list of the codes for each character:

Character	Frequency/count	Code
a	4	01
b	7	11
c	3	101
d	2	100
e	4	00

Below is implementation in C programming:

// C program for Huffman Coding
#include <stdio.h>
#include <stdlib.h>

// This constant can be avoided by explicitly
// calculating height of Huffman Tree
#define MAX_TREE_HT 100

// A Huffman tree node
struct MinHeapNode {

	// One of the input characters
	char data;

	// Frequency of the character
	unsigned freq;

	// Left and right child of this node
	struct MinHeapNode *left, *right;
};

// A Min Heap: Collection of
// min-heap (or Huffman tree) nodes
struct MinHeap {

	// Current size of min heap
	unsigned size;

	// capacity of min heap
	unsigned capacity;

	// Array of minheap node pointers
	struct MinHeapNode** array;
};

// A utility function allocate a new
// min heap node with given character
// and frequency of the character
struct MinHeapNode* newNode(char data, unsigned freq)
{
	struct MinHeapNode* temp = (struct MinHeapNode*)malloc(
		sizeof(struct MinHeapNode));

	temp->left = temp->right = NULL;
	temp->data = data;
	temp->freq = freq;

	return temp;
}

// A utility function to create
// a min heap of given capacity
struct MinHeap* createMinHeap(unsigned capacity)

{

	struct MinHeap* minHeap
		= (struct MinHeap*)malloc(sizeof(struct MinHeap));

	// current size is 0
	minHeap->size = 0;

	minHeap->capacity = capacity;

	minHeap->array = (struct MinHeapNode**)malloc(
		minHeap->capacity * sizeof(struct MinHeapNode*));
	return minHeap;
}

// A utility function to
// swap two min heap nodes
void swapMinHeapNode(struct MinHeapNode** a,
					struct MinHeapNode** b)

{

	struct MinHeapNode* t = *a;
	*a = *b;
	*b = t;
}

// The standard minHeapify function.
void minHeapify(struct MinHeap* minHeap, int idx)

{

	int smallest = idx;
	int left = 2 * idx + 1;
	int right = 2 * idx + 2;

	if (left < minHeap->size
		&& minHeap->array[left]->freq
			< minHeap->array[smallest]->freq)
		smallest = left;

	if (right < minHeap->size
		&& minHeap->array[right]->freq
			< minHeap->array[smallest]->freq)
		smallest = right;

	if (smallest != idx) {
		swapMinHeapNode(&minHeap->array[smallest],
						&minHeap->array[idx]);
		minHeapify(minHeap, smallest);
	}
}

// A utility function to check
// if size of heap is 1 or not
int isSizeOne(struct MinHeap* minHeap)
{

	return (minHeap->size == 1);
}

// A standard function to extract
// minimum value node from heap
struct MinHeapNode* extractMin(struct MinHeap* minHeap)

{

	struct MinHeapNode* temp = minHeap->array[0];
	minHeap->array[0] = minHeap->array[minHeap->size - 1];

	--minHeap->size;
	minHeapify(minHeap, 0);

	return temp;
}

// A utility function to insert
// a new node to Min Heap
void insertMinHeap(struct MinHeap* minHeap,
				struct MinHeapNode* minHeapNode)

{

	++minHeap->size;
	int i = minHeap->size - 1;

	while (i
		&& minHeapNode->freq
				< minHeap->array[(i - 1) / 2]->freq) {

		minHeap->array[i] = minHeap->array[(i - 1) / 2];
		i = (i - 1) / 2;
	}

	minHeap->array[i] = minHeapNode;
}

// A standard function to build min heap
void buildMinHeap(struct MinHeap* minHeap)

{

	int n = minHeap->size - 1;
	int i;

	for (i = (n - 1) / 2; i >= 0; --i)
		minHeapify(minHeap, i);
}

// A utility function to print an array of size n
void printArr(int arr[], int n)
{
	int i;
	for (i = 0; i < n; ++i)
		printf("%d", arr[i]);

	printf("\n");
}

// Utility function to check if this node is leaf
int isLeaf(struct MinHeapNode* root)

{

	return !(root->left) && !(root->right);
}

// Creates a min heap of capacity
// equal to size and inserts all character of
// data[] in min heap. Initially size of
// min heap is equal to capacity
struct MinHeap* createAndBuildMinHeap(char data[],
									int freq[], int size)

{

	struct MinHeap* minHeap = createMinHeap(size);

	for (int i = 0; i < size; ++i)
		minHeap->array[i] = newNode(data[i], freq[i]);

	minHeap->size = size;
	buildMinHeap(minHeap);

	return minHeap;
}

// The main function that builds Huffman tree
struct MinHeapNode* buildHuffmanTree(char data[],
									int freq[], int size)

{
	struct MinHeapNode *left, *right, *top;

	// Step 1: Create a min heap of capacity
	// equal to size. Initially, there are
	// modes equal to size.
	struct MinHeap* minHeap
		= createAndBuildMinHeap(data, freq, size);

	// Iterate while size of heap doesn't become 1
	while (!isSizeOne(minHeap)) {

		// Step 2: Extract the two minimum
		// freq items from min heap
		left = extractMin(minHeap);
		right = extractMin(minHeap);

		// Step 3: Create a new internal
		// node with frequency equal to the
		// sum of the two nodes frequencies.
		// Make the two extracted node as
		// left and right children of this new node.
		// Add this node to the min heap
		// '$' is a special value for internal nodes, not
		// used
		top = newNode('$', left->freq + right->freq);

		top->left = left;
		top->right = right;

		insertMinHeap(minHeap, top);
	}

	// Step 4: The remaining node is the
	// root node and the tree is complete.
	return extractMin(minHeap);
}

// Prints huffman codes from the root of Huffman Tree.
// It uses arr[] to store codes
void printCodes(struct MinHeapNode* root, int arr[],
				int top)

{

	// Assign 0 to left edge and recur
	if (root->left) {

		arr[top] = 0;
		printCodes(root->left, arr, top + 1);
	}

	// Assign 1 to right edge and recur
	if (root->right) {

		arr[top] = 1;
		printCodes(root->right, arr, top + 1);
	}

	// If this is a leaf node, then
	// it contains one of the input
	// characters, print the character
	// and its code from arr[]
	if (isLeaf(root)) {

		printf("%c: ", root->data);
		printArr(arr, top);
	}
}

// The main function that builds a
// Huffman Tree and print codes by traversing
// the built Huffman Tree
void HuffmanCodes(char data[], int freq[], int size)

{
	// Construct Huffman Tree
	struct MinHeapNode* root
		= buildHuffmanTree(data, freq, size);

	// Print Huffman codes using
	// the Huffman tree built above
	int arr[MAX_TREE_HT], top = 0;

	printCodes(root, arr, top);
}
// Driver code
int main()
{
	char arr[] = { 'a', 'b', 'c', 'd', 'e', 'f' };
	int freq[] = { 5, 9, 12, 13, 16, 45 };
	int size = sizeof(arr) / sizeof(arr[0]);
	HuffmanCodes(arr, freq, size);
	return 0;
}

Output

f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111
……………
Process executed in 1.11 seconds
Press any key to continue.

Java Implementation of above code:

import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Scanner;

class Huffman {

	// recursive function to print the
	// huffman-code through the tree traversal.
	// Here s is the huffman - code generated.
	public static void printCode(HuffmanNode root, String s)
	{

		// base case; if the left and right are null
		// then its a leaf node and we print
		// the code s generated by traversing the tree.
		if (root.left == null && root.right == null
			&& Character.isLetter(root.c)) {

			// c is the character in the node
			System.out.println(root.c + ":" + s);

			return;
		}

		// if we go to left then add "0" to the code.
		// if we go to the right add"1" to the code.

		// recursive calls for left and
		// right sub-tree of the generated tree.
		printCode(root.left, s + "0");
		printCode(root.right, s + "1");
	}

	// main function
	public static void main(String[] args)
	{
		Scanner s = new Scanner(System.in);
		// number of characters.
		int n = 6;
		char[] charArray = { 'a', 'b', 'c', 'd', 'e', 'f' };
		int[] charfreq = { 5, 9, 12, 13, 16, 45 };

		// creating a priority queue q.
		// makes a min-priority queue(min-heap).
		PriorityQueue<HuffmanNode> q
			= new PriorityQueue<HuffmanNode>(
				n, new MyComparator());

		for (int i = 0; i < n; i++) {

			// creating a Huffman node object
			// and add it to the priority queue.
			HuffmanNode hn = new HuffmanNode();

			hn.c = charArray[i];
			hn.data = charfreq[i];

			hn.left = null;
			hn.right = null;

			// add functions adds
			// the huffman node to the queue.
			q.add(hn);
		}

		// create a root node
		HuffmanNode root = null;

		// Here we will extract the two minimum value
		// from the heap each time until
		// its size reduces to 1, extract until
		// all the nodes are extracted.
		while (q.size() > 1) {

			// first min extract.
			HuffmanNode x = q.peek();
			q.poll();

			// second min extract.
			HuffmanNode y = q.peek();
			q.poll();

			// new node f which is equal
			HuffmanNode f = new HuffmanNode();

			// to the sum of the frequency of the two nodes
			// assigning values to the f node.
			f.data = x.data + y.data;
			f.c = '-';

			// first extracted node as left child.
			f.left = x;

			// second extracted node as the right child.
			f.right = y;

			// marking the f node as the root node.
			root = f;

			// add this node to the priority-queue.
			q.add(f);
		}

		// print the codes by traversing the tree
		printCode(root, "");
	}
}
// node class is the basic structure
// of each node present in the Huffman - tree.
class HuffmanNode {

	int data;
	char c;

	HuffmanNode left;
	HuffmanNode right;
}
// comparator class helps to compare the node
// on the basis of one of its attribute.
// Here we will be compared
// on the basis of data values of the nodes.
class MyComparator implements Comparator<HuffmanNode> {
	public int compare(HuffmanNode x, HuffmanNode y)
	{

		return x.data - y.data;
	}
}

Output

f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111
……………….
Process executed in 1.11 seconds
Press any key to continue.

Explanation:

By traversing, the Huffman Tree is created and decoded. The values gathered during the traversal are then to be applied to the character located at the leaf node. Every unique character in the supplied stream of data may be identified using the Huffman Code in this manner. O (nlogn), where n is the total number of characters, is the time complexity. ExtractMin() is called 2*(n - 1) times if there are n nodes. Since extractMin() calls minHeapify(), its execution time is O (logn). The total complexity is therefore O (nlogn). There is a linear time algorithm if the input array is sorted. This will be covered in more detail in our upcoming piece.

Problems with Huffman Coding

Let's talk about the drawbacks of Huffman coding in this part and why it isn't always the best option:

If not all of the characters' probabilities or frequencies are negative powers of 2, it is not regarded as ideal.
Although one may get closer to the ideal by grouping symbols and expanding the alphabet, the blocking method necessitates handling a larger alphabet. Therefore, Huffman coding may not always be very effective.
Although there are many effective ways to count the frequency of each symbol or character, reconstructing the entire tree for each one can be very time-consuming. When the alphabet is large and the probability distributions change quickly with each symbol, this is typically the case.

Greedy Huffman Code Construction Algorithm

Huffman developed a greedy technique that generates a Huffman Code, an ideal prefix code, for each distinct character in the input data stream.
The approach uses the fewest nodes each time to create the Huffman tree from the bottom up.
Because each character receives a length of code based on how frequently it appears in the given stream of data, this method is known as a greedy approach. It is a commonly occurring element in the data if the size of the code retrieved is less.

The use of Huffman Coding

Here, we'll talk about some practical uses for Huffman Coding:
Conventional compression formats like PKZIP, GZIP, etc. typically employ Huffman coding.
Huffman Coding is used for data transfer by fax and text because it minimizes file size and increases transmission speed.
Huffman encoding (particularly the prefix codes) is used by several multimedia storage formats, including JPEG, PNG, and MP3, to compress the files.
Huffman Coding is mostly used for image compression.
When a string of often recurring characters has to be sent, it can be more helpful.

Conclusion

In general, Huffman Coding is helpful for compressing data that contains frequently occurring characters.
We can see that the character that occurs most frequently has the shortest code, whereas the one that occurs the least frequently has the greatest code.
The Huffman Code compression technique is used to create variable-length coding, which uses a varied amount of bits for each letter or symbol. This method is superior to fixed-length coding since it uses less memory and transmits data more quickly.
Go through this article to have a better knowledge of the greedy algorithm.

Next TopicKadane's Algorithm

← prev next →