Wildcard Pattern MatchingSuppose we have a string and a pattern then we have to compare the string with a pattern that whether the pattern matches with a string or not. Here we are looking for the complete match not for the partial match. Th given text and wildcard pattern implement the wildcard pattern matching algorithm to find the match. This algorithm finds the complete match not the partial match. The wildcard pattern contains the following two special characters:
Let's understand through the examples. Example 1: Suppose the pattern is (a * b) Pattern: a * b If the string is "ab" The pattern starts with 'a' character and ends with 'b' character. Between 'a' and 'b', we ca use any of the characters. Since the string starts with a 'a' and ends with 'b' and does not contain any character between 'a' and 'b'; therefore, the string completely matches with a pattern. If the string is "aab" The string starts with a 'a' and ends with a 'b' character, and contains 'a' character between 'a' and 'b'. According to the pattern specified, we can use any of the characters in between 'a' and 'b'; therefore, the above string completely matches with a specified pattern. If the string is "a" Since the string does not end with a character 'b'; therefore, the above string does not match with the specified pattern. So, it returns a false value. If the string is "abc" Since the string ends with a 'c' character rather than the 'b' character; therefore, the string does not match completely with a specified pattern. So, it returns a false value. Pattern is "a ? b" The above pattern specifies that the string should start with 'a' and ends with 'b' character. The string should exactly contain any one character between 'a' and 'b'. If the string is "aab" Since the string starts with 'a' and ends with 'b' character, and contain exactly single character between 'a' and 'b'; therefore, the string completely satisfies the specified pattern. If the string is "ab" Since the string starts with 'a' and ends with 'b' but does not contain any character between 'a' and 'b', so string does not completely match with a pattern. It returns a false value. Pattern is: x ? y * z The above pattern specifies that there can be any single character between x and y, 0 or any sequence of characters can exist between y and z. If the string is "xayz" In the given string, only one character exists between 'x' and 'y', and no single character exists between 'y' and 'z'; therefore, the string completely matches with a pattern. If the string is "xyz" In the given string, no single character exists between 'x' and 'y'; therefore, the given string does not completely match with a specified pattern. Here we will use the dynamic programming approach to solve the problem. 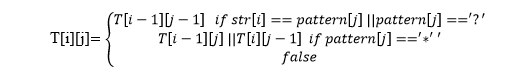
In the above equation, 'T' is the two dimensional array and T[i][j] is the substring in the string from 0 to i and 0 to j represents the pattern. Let's understand in the tabular form.
When i=0, j = 0
When i=0, j = (0 to 5)
When i=1, j=0
When i=1, j=1
Since T[i] = =T[j], i.e., x==x; therefore, the first condition is satisfied. According to the first condition, we will take T[i-1][j-1], i.e., diagonal value. So, T[1][1] = T as shown in the above table. When i=1, j=2
In this case, string is 'x' and pattern is "x ?". T[i-1][j-1] equals to 'x' so it returns false value. When i=1, j=3
Since 'x' is not equal to 'y' so we will get false at T[1][3]. When i=1, j=4
As we can observe in the above table that '*' is the pattern. According to the condition 3, we will look at the value on the left and on the top. Since the value on both the sides is false; therefore, the value at T[1][4] is also false. When i=1, j=5
Since the value at T[1] is not equal to T[5], i.e., x!=z; therefore, the value at T[1][5] is also false. When i=2, j=1
Now the string is "xa" and the pattern is 'x'. Since both are not same; therefore, the value at T[2][1] is false. When i=2, j=2
Now the string is "xa" and the pattern is "x?". When we compare "xa" and "x?" then 'x' is matched with 'x', and '?' means exactly one character exists after 'x' character. In the string "xa", 'a' character exists after 'x'. Therefore, the string completely matches with a pattern. When i=2, j=3
As we can observe in the above table that T[2] is 'a' and T[3] = 'y'; Since both the characters are different so the value at T[2][3] is false. When i=2, j=4
Since the pattern is '*' so according to the condition 2, we will look at the values on the left and top. Since the values on both the sides is false; therefore the value at T[2][4] is also false. When i=2, j=5
Since the value at T[i] is not equal to T[j], i.e., a !=z; therefore, the value at T[2][5] is equal to false. When i=3, j=1
The value of T[3] is 'y' and the value of T[1] is 'x'. Since both the values are different so the value at T[3][1] would be false. When i=3, j=2
Here, the pattern is "x?" and the string is "xay". The '?' matches with 'y' but "xa" and 'x' does not match so we consider the diagonal value, i.e., false. Therefore, the value at T[3][2] would also be false. When i=3, j=3
In this case, the pattern is "x?y" and the string is "xay". When we compare both the pattern and the string, 'x' matches with 'x', '?' matches with 'a', and 'y' matches with 'y'. Therefore, we can say that the string completely matches with a pattern, and the value at T[3][3] would be true. When i=3, j=4
In this case, the string is "xay" and the pattern is "x?y*". The '*' matches with 0 or more sequence of characters. We look at the values on the left and top. Since the value on the left is true; therefore the value at T[3][4] is true. When i=3, j=5
Since 'y' does not match with a 'z' so the value at T[3][5] would be false. When i=4, j=1
Since 'l' does not match with a 'x' so the value at T[3][1] would be false. When i=4, j=2
Now the pattern is '?', so we will consider the diagonal value. The diagonal value is false so the value at T[3][2] would also be false. When i=4, j=3
Here, T[3] = 'l' and T[3] = 'y'. Since both are the different characters so the value at T[3][3] would be false. When i=4, j=4
Here, T[j] = '*'. In this case, we will look at the values on the left and top. Since the value on the top is true so the value at T[3][4] would also be true. When i=4, j=5
The value of T[4] is 'l', and the value of T[5] is 'z'. Since 'l' is not equal to 'z' so the value at T[4][5] would be false. When i=5, j=1
The value of T[5] is 'm' and the value of T[1] is 'x'. Since 'm' is not equal to 'x' so the value at T[5][1] would be false. When i=5, j=2
In this case, pattern[j] is '?', so we will consider the diagonal value. Since the diagonal value is 'false', so the value at T[5][2] would also be false. When i=5, j=3
In this case, the value of T[5] is 'm' and the value of T[3] is 'y'. Since the both the values are different so the value at T[5][3] would be false. When i=5, j=4
Here, the pattern[j] is '*'. We will look at the values on the left and right. The value of the top is false so the value at T[5][4] would also be true. When i=5, j=5
The value at T[5] is 'm' and the value at T[5] is 'z'. Since both the values are different, so the value at T[5][5] would be false. Similarly, we will perform the operations on the last row. The table can be represented as:
In the last row and the last column, we get the true value. Therefore, the final value is true so the given string completely matches the pattern. Implementation of Wildcard pattern matching in C++ Output 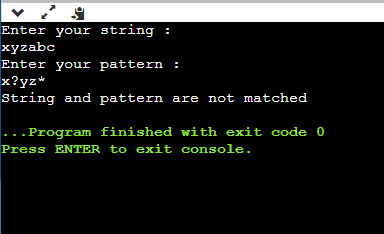
Next TopicLargest Sum Contiguous Subarray
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









