Algorithm of Matrix Chain Multiplication
We will use table s to construct an optimal solution. Step 1: Constructing an Optimal Solution:
PRINT-OPTIMAL-PARENS (s, i, j)
1. if i=j
2. then print "A"
3. else print "("
4. PRINT-OPTIMAL-PARENS (s, i, s [i, j])
5. PRINT-OPTIMAL-PARENS (s, s [i, j] + 1, j)
6. print ")"
Analysis: There are three nested loops. Each loop executes a maximum n times.
Body of loop constant complexity Total Complexity is: O (n3) Algorithm with Explained ExampleQuestion: P [7, 1, 5, 4, 2} Solution: Here, P is the array of a dimension of matrices. So here we will have 4 matrices:
A17x1 A21x5 A35x4 A44x2
i.e.
First Matrix A1 have dimension 7 x 1
Second Matrix A2 have dimension 1 x 5
Third Matrix A3 have dimension 5 x 4
Fourth Matrix A4 have dimension 4 x 2
Let say,
From P = {7, 1, 5, 4, 2} - (Given)
And P is the Position
p0 = 7, p1 =1, p2 = 5, p3 = 4, p4=2.
Length of array P = number of elements in P
∴length (p)= 5
From step 3
Follow the steps in Algorithm in Sequence
According to Step 1 of Algorithm Matrix-Chain-Order
Step 1:
n ← length [p]-1
Where n is the total number of elements
And length [p] = 5
∴ n = 5 - 1 = 4
n = 4
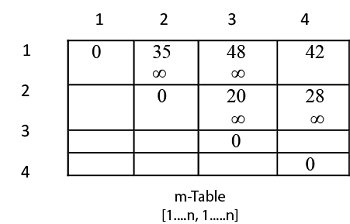
Now we construct two tables m and s.
Table m has dimension [1.....n, 1.......n]
Table s has dimension [1.....n-1, 2.......n]
Now, according to step 2 of Algorithm Case 1: 1. When l - 2
for (i ← 1 to n - l + 1)
i ← 1 to 4 - 2 + 1
i ← 1 to 3
When i = 1
do j ← i + l - 1
j ← 1 + 2 - 1
j ← 2
i.e. j = 2
Now, m [i, j] ← ∞
i.e. m [1,2] ← ∞
Put ∞ in m [1, 2] table
for k ← i to j-1
k ← 1 to 2 - 1
k ← 1 to 1
k = 1
Now q ← m [i, k] + m [k + 1, j] + pi-1 pk pj
for l = 2
i = 1
j =2
k = 1
q ← m [1,1] + m [2,2] + p0x p1x p2
and m [1,1] = 0
for i ← 1 to 4
∴ q ← 0 + 0 + 7 x 1 x 5
q ← 35
We have m [i, j] = m [1, 2] = ∞
Comparing q with m [1, 2]
q < m [i, j]
i.e. 35 < m [1, 2]
35 < ∞
True
then, m [1, 2 ] ← 35 (∴ m [i,j] ← q)
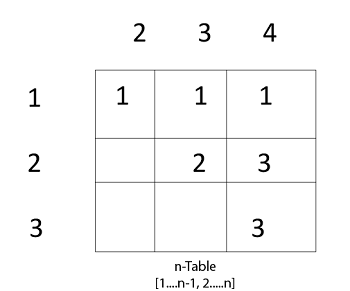
s [1, 2] ← k
and the value of k = 1
s [1,2 ] ← 1
Insert "1" at dimension s [1, 2] in table s. And 35 at m [1, 2]
2. l remains 2
L = 2
i ← 1 to n - l + 1
i ← 1 to 4 - 2 + 1
i ← 1 to 3
for i = 1 done before
Now value of i becomes 2
i = 2
j ← i + l - 1
j ← 2 + 2 - 1
j ← 3
j = 3
m [i , j] ← ∞
i.e. m [2,3] ← ∞
Initially insert ∞ at m [2, 3]
Now, for k ← i to j - 1
k ← 2 to 3 - 1
k ← 2 to 2
i.e. k =2
Now, q ← m [i, k] + m [k + 1, j] + pi-1 pk pj
For l =2
i = 2
j = 3
k = 2
q ← m [2, 2] + m [3, 3] + p1x p2 x p3
q ← 0 + 0 + 1 x 5 x 4
q ← 20
Compare q with m [i ,j ]
If q < m [i,j]
i.e. 20 < m [2, 3]
20 < ∞
True
Then m [i,j ] ← q
m [2, 3 ] ← 20
and s [2, 3] ← k
and k = 2
s [2,3] ← 2
3. Now i become 3
i = 3
l = 2
j ← i + l - 1
j ← 3 + 2 - 1
j ← 4
j = 4
Now, m [i, j ] ← ∞
m [3,4 ] ← ∞
Insert ∞ at m [3, 4]
for k ← i to j - 1
k ← 3 to 4 - 1
k ← 3 to 3
i.e. k = 3
Now, q ← m [i, k] + m [k + 1, j] + pi-1 pk pj
i = 3
l = 2
j = 4
k = 3
q ← m [3, 3] + m [4,4] + p2 x p3 x p4
q ← 0 + 0 + 5 x 2 x 4
q 40
Compare q with m [i, j]
If q < m [i, j]
40 < m [3, 4]
40 < ∞
True
Then, m [i,j] ← q
m [3,4] ← 40
and s [3,4] ← k
s [3,4] ← 3
Case 2: l becomes 3
L = 3
for i = 1 to n - l + 1
i = 1 to 4 - 3 + 1
i = 1 to 2
When i = 1
j ← i + l - 1
j ← 1 + 3 - 1
j ← 3
j = 3
Now, m [i,j] ← ∞
m [1, 3] ← ∞
for k ← i to j - 1
k ← 1 to 3 - 1
k ← 1 to 2
Now we compare the value for both k=1 and k = 2. The minimum of two will be placed in m [i,j] or s [i,j] respectively. 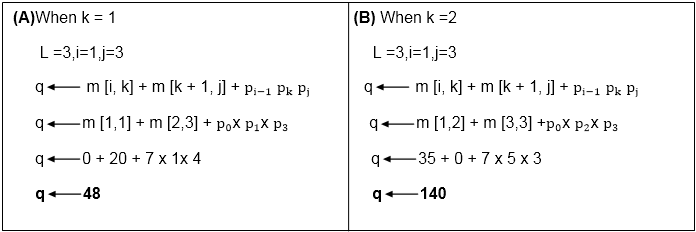
Now from above
Value of q become minimum for k=1
∴ m [i,j] ← q
m [1,3] ← 48
Also m [i,j] > q
i.e. 48 < ∞
∴ m [i , j] ← q
m [i, j] ← 48
and s [i,j] ← k
i.e. m [1,3] ← 48
s [1, 3] ← 1
Now i become 2
i = 2
l = 3
then j ← i + l -1
j ← 2 + 3 - 1
j ← 4
j = 4
so m [i,j] ← ∞
m [2,4] ← ∞
Insert initially ∞ at m [2, 4]
for k ← i to j-1
k ← 2 to 4 - 1
k ← 2 to 3
Here, also find the minimum value of m [i,j] for two values of k = 2 and k =3 
Case 3: l becomes 4
L = 4
For i ← 1 to n-l + 1
i ← 1 to 4 - 4 + 1
i ← 1
i = 1
do j ← i + l - 1
j ← 1 + 4 - 1
j ← 4
j = 4
Now m [i,j] ← ∞
m [1,4] ← ∞
for k ← i to j -1
k ← 1 to 4 - 1
k ← 1 to 3
When k = 1
q ← m [i, k] + m [k + 1, j] + pi-1 pk pj
q ← m [1,1] + m [2,4] + p0xp4x p1
q ← 0 + 28 + 7 x 2 x 1
q ← 42
Compare q and m [i, j]
m [i,j] was ∞
i.e. m [1,4]
if q < m [1,4]
42< ∞
True
Then m [i,j] ← q
m [1,4] ← 42
and s [1,4] 1 ? k =1
When k = 2
L = 4, i=1, j = 4
q ← m [i, k] + m [k + 1, j] + pi-1 pk pj
q ← m [1, 2] + m [3,4] + p0 xp2 xp4
q ← 35 + 40 + 7 x 5 x 2
q ← 145
Compare q and m [i,j]
Now m [i, j]
i.e. m [1,4] contains 42.
So if q < m [1, 4]
But 145 less than or not equal to m [1, 4]
So 145 less than or not equal to 42.
So no change occurs.
When k = 3
l = 4
i = 1
j = 4
q ← m [i, k] + m [k + 1, j] + pi-1 pk pj
q ← m [1, 3] + m [4,4] + p0 xp3 x p4
q ← 48 + 0 + 7 x 4 x 2
q ← 114
Again q less than or not equal to m [i, j]
i.e. 114 less than or not equal to m [1, 4]
114 less than or not equal to 42
So no change occurs. So the value of m [1, 4] remains 42. And value of s [1, 4] = 1 Now we will make use of only s table to get an optimal solution. 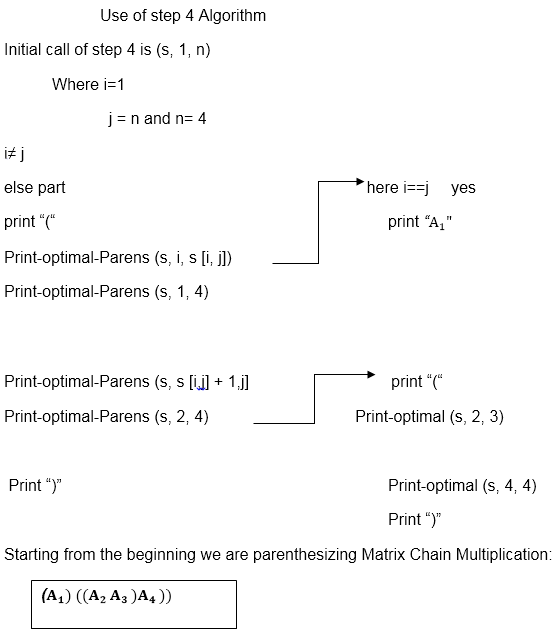
Next TopicLongest Common Sequence
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










