Methods of Hashing

There are two main methods used to implement hashing:

1. Hashing with Chaining
2. Hashing with open addressing

1. Hashing with Chaining

In Hashing with Chaining, the element in S is stored in Hash table T [0...m-1] of size m, where m is somewhat larger than n, the size of S. The hash table is said to have m slots. Associated with the hashing scheme is a hash function h which is mapping from U to {0...m-1}.Each key k ∈S is stored in location T [h (k)], and we say that k is hashed into slot h (k). If more than one key in S hashed into the same slot then we have a collision.

In such case, all keys that hash into the same slot are placed in a linked list associated with that slot, this linked list is called the chain at slot. The load factor of a hash table is defined to be ∝=n/m it represents the average number of keys per slot. We typically operate in the range m=θ(n), so ∝ is usually a constant generally ∝<1.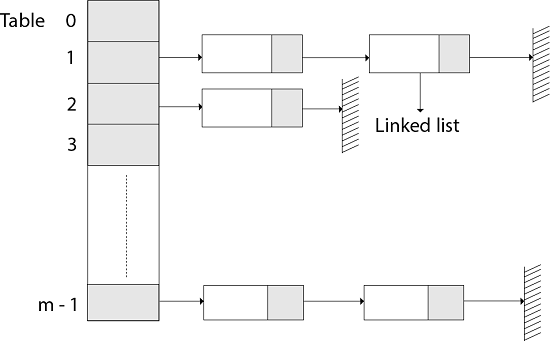

Collision Resolution by Chaining:

In chaining, we place all the elements that hash to the same slot into the same linked list, As fig shows that Slot j contains a pointer to the head of the list of all stored elements that hash to j ; if there are no such elements, slot j contains NIL.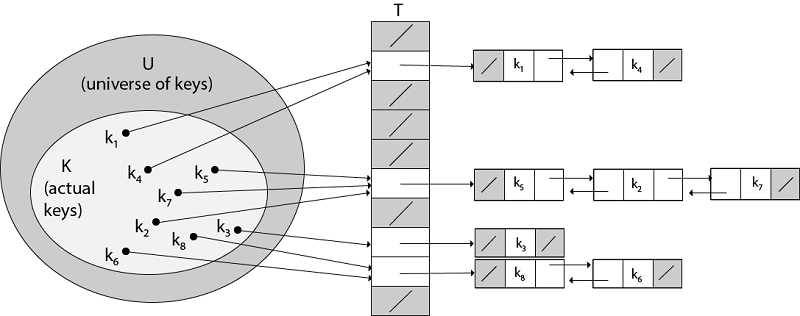

Fig: Collision resolution by chaining.

Each hash-table slot T [j] contains a linked list of all the keys whose hash value is j.

For example, h (k1) = h (k4) and h (k5) = h (k7) =h (K2). The linked list can be either singly or doubly linked; we show it as doubly linked because deletion is faster that way.

Analysis of Hashing with Chaining:

Given a hash table T with m slots that stores n elements, we define the load factors α for T as n/m that is the average number of elements stored in a chain. The worst case running time for searching is thus θ(n) plus the time to compute the hash function- no better than if we used one linked list for all the elements. Clearly, hash tables are not used for their worst-case performance.

The average performance of hashing depends on how well the hash function h distributes the set of keys to be stored among the m slots, on the average.

Example: let us consider the insertion of elements 5, 28, 19,15,20,33,12,17,10 into a chained hash table. Let us suppose the hash table has 9 slots and the hash function be h (k) =k mod 9.

Solution: The initial state of chained-hash table

Insert 5:

Create a linked list for T [5] and store value 5 in it.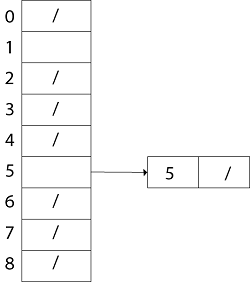

Similarly, insert 28. h (28) = 28 mod 9 =1. Create a Linked List for T [1] and store value 28 in it. Now insert 19 h (19) = 19 mod 9 = 1. Insert value 19 in the slot T [1] at the beginning of the linked-list.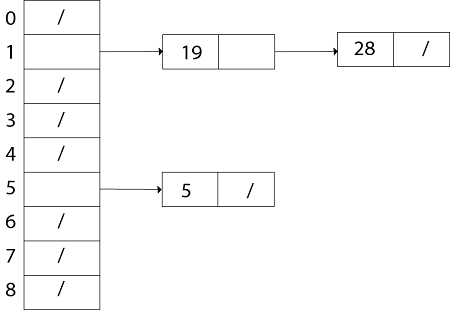

Thus the chained- hash- table after inserting key 10 is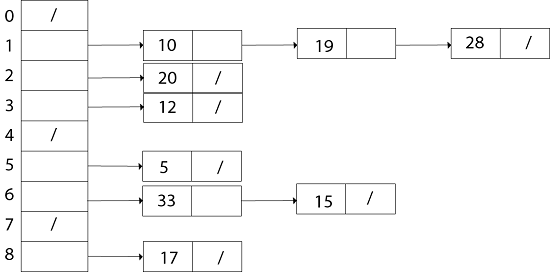

2. Hashing with Open Addressing

In Open Addressing, all elements are stored in hash table itself. That is, each table entry consists of a component of the dynamic set or NIL. When searching for an item, we consistently examine table slots until either we find the desired object or we have determined that the element is not in the table. Thus, in open addressing, the load factor α can never exceed 1.

The advantage of open addressing is that it avoids Pointer. In this, we compute the sequence of slots to be examined. The extra memory freed by not sharing pointers provides the hash table with a larger number of slots for the same amount of memory, potentially yielding fewer collision and faster retrieval.

The process of examining the location in the hash table is called Probing.

Thus, the hash function becomes

With open addressing, we require that for every key k, the probe sequence

The HASH-INSERT procedure takes as input a hash table T and a key k

HASH-INSERT (T, k)
 1. i ← 0
 2. repeat j ← h (k, i)
 3. if T [j] = NIL
 4. then T [j] ← k
 5. return j
 6. else ← i= i +1
 7. until i=m
 8. error "hash table overflow"

The procedure HASH-SEARCH takes as input a hash table T and a key k, returning j if it finds that slot j contains key k or NIL if key k is not present in table T.

HASH-SEARCH.T (k)
 1. i ← 0
 2. repeat j ← h (k, i)
 3. if T [j] =j
 4. then return j
 5. i ← i+1
 6. until T [j] = NIL or i=m
 7. return NIL