Polynomial Time Verification

Before talking about the class of NP-complete problems, it is essential to introduce the notion of a verification algorithm.

Many problems are hard to solve, but they have the property that it easy to authenticate the solution if one is provided.

Hamiltonian cycle problem:-

Consider the Hamiltonian cycle problem. Given an undirected graph G, does G have a cycle that visits each vertex exactly once? There is no known polynomial time algorithm for this dispute.

Note: - It means you can't build a Hamiltonian cycle in a graph with a polynomial time even if there is no specific path is given for the Hamiltonian cycle with the particular vertex, yet you can't verify the Hamiltonian cycle within the polynomial time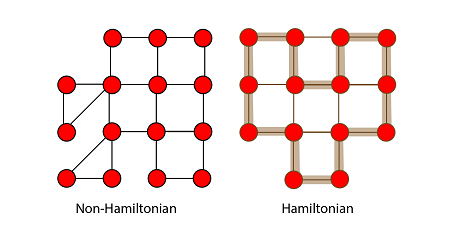

Fig: Hamiltonian Cycle

Let us understand that a graph did have a Hamiltonian cycle. It would be easy for someone to convince of this. They would similarly say: "the period is hv3, v7, v1....v13i.

We could then inspect the graph and check that this is indeed a legal cycle and that it visits all of the vertices of the graph exactly once. Thus, even though we know of no efficient way to solve the Hamiltonian cycle problem, there is a beneficial way to verify that a given cycle is indeed a Hamiltonian cycle.

Note:-For the verification in the Polynomial-time of an undirected Hamiltonian cycle graph G. There must be exact/specific/definite path must be given of Hamiltonian cycle then you can verify in the polynomial time.

Definition of Certificate: - A piece of information which contains in the given path of a vertex is known as certificate

Relation of P and NP classes

1. P contains in NP
2. P=NP

1. Observe that P contains in NP. In other words, if we can solve a problem in polynomial time, we can indeed verify the solution in polynomial time. More formally, we do not need to see a certificate (there is no need to specify the vertex/intermediate of the specific path) to solve the problem; we can explain it in polynomial time anyway.
2. However, it is not known whether P = NP. It seems you can verify and produce an output of the set of decision-based problems in NP classes in a polynomial time which is impossible because according to the definition of NP classes you can verify the solution within the polynomial time. So this relation can never be held.

Reductions:

The class NP-complete (NPC) problems consist of a set of decision problems (a subset of class NP) that no one knows how to solve efficiently. But if there were a polynomial solution for even a single NP-complete problem, then every problem in NPC will be solvable in polynomial time. For this, we need the concept of reductions.

Suppose there are two problems, A and B. You know that it is impossible to solve problem A in polynomial time. You want to prove that B cannot be explained in polynomial time. We want to show that (A ∉ P) => (B ∉ P)

Consider an example to illustrate reduction: The following problem is well-known to be NPC:

3-color: Given a graph G, can each of its vertices be labeled with one of 3 different colors such that two adjacent vertices do not have the same label (color).

Coloring arises in various partitioning issues where there is a constraint that two objects cannot be assigned to the same set of partitions. The phrase "coloring" comes from the original application which was in map drawing. Two countries that contribute a common border should be colored with different colors.

It is well known that planar graphs can be colored (maps) with four colors. There exists a polynomial time algorithm for this. But deciding whether this can be done with 3 colors is hard, and there is no polynomial time algorithm for it.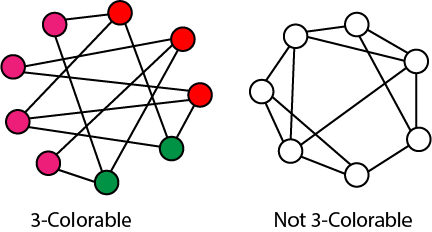

Fig: Example of 3-colorable and non-3-colorable graphs.

Polynomial Time Reduction:

We say that Decision Problem L₁ is Polynomial time Reducible to decision Problem L₂ (L_1≤p L₂) if there is a polynomial time computation function f such that of all x, xϵL₁ if and only if xϵL₂.