Binary Search Trees

A Binary Search tree is organized in a Binary Tree. Such a tree can be defined by a linked data structure in which a particular node is an object. In addition to a key field, each node contains field left, right, and p that point to the nodes corresponding to its left child, its right child, and its parent, respectively. If a child or parent is missing, the appropriate field contains the value NIL. The root node is the only node in the tree whose parent field is Nil.

Binary Search Tree Property

Let x be a node in a binary search tree.

• If y is a node in the left subtree of x, then key [y] ≤key [k].
• If z is a node in the right subtree of x, then key [x] ≤ key [y].

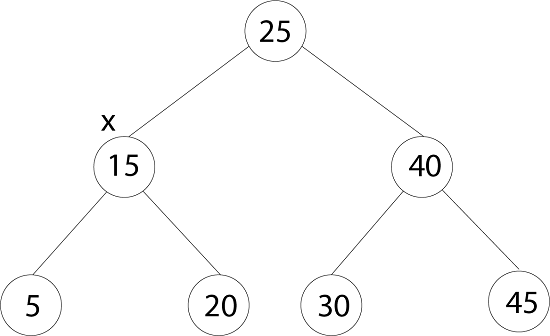
In this tree key [x] = 15

• If y is a node in the left subtree of x, then key [y] = 5.

• If y is a node in the right subtree of x, then key [y] = 20.

Traversal in Binary Search Trees:

1. In-Order-Tree-Walk (x): Always prints keys in binary search tree in sorted order.

INORDER-TREE-WALK (x) - Running time is θ(n)
 1. If x ≠ NIL.
 2. then INORDER-TREE-WALK (left [x])
 3. print key [x]
 4. INORDER-TREE-WALK (right [x])

2. PREORDER-TREE-WALK (x): In which we visit the root node before the nodes in either subtree.

PREORDER-TREE-WALK (x): 
 1. If x ≠ NIL.
 2. then print key [x]
 3. PREORDER-TREE-WALK (left [x]).
 4. PREORDER-TREE-WALK (right [x]).

3. POSTORDER-TREE-WALK (x): In which we visit the root node after the nodes in its subtree.

POSTORDER-TREE-WALK (x): 
 1. If x ≠ NIL.
 2. then POSTORDER-TREE-WALK (left [x]).
 3. POSTORDER-TREE-WALK (right [x]).
 4. print key [x]

Querying a Binary Search Trees:

1. Searching: The TREE-SEARCH (x, k) algorithm searches the tree node at x for a node whose key value equal to k. It returns a pointer to the node if it exists otherwise NIL.

TREE-SEARCH (x, k)
 1. If x = NIL or k = key [x].
 2. then return x.
 3. If k < key [x].
 4. then return TREE-SEARCH (left [x], k)
 5. else return TREE-SEARCH (right [x], k)

Clearly, this algorithm runs in O (h) time where h is the height of the tree. The iterative version of the above algorithm is very easy to implement

ITERATIVE-TREE- SEARCH (x, k)
 1. while x ≠ NIL and k ≠ key [k].
 2. do if k < key [x].
 3. then x ← left [x].
 4. else x ← right [x].
 5. return x.

2. Minimum and Maximum: An item in a binary search tree whose key is a minimum can always be found by following left child pointers from the root until a NIL is encountered. The following procedure returns a pointer to the minimum element in the subtree rooted at a given node x.

TREE- MINIMUM (x)
 1. While left [x] ≠ NIL.
 2. do x←left [x].
 3. return x.

TREE-MAXIMUM (x)
 1. While left [x] ≠ NIL
 2. do x←right [x].
 3. return x.

3. Successor and predecessor: Given a node in a binary search tree, sometimes we used to find its successor in the sorted form determined by an in order tree walk. If all keys are specific, the successor of a node x is the node with the smallest key greater than key[x]. The structure of a binary search tree allows us to rule the successor of a node without ever comparing keys. The following action returns the successor of a node x in a binary search tree if it exists, and NIL if x has the greatest key in the tree:

TREE SUCCESSOR (x)
 1. If right [x] ≠ NIL.
 2. Then return TREE-MINIMUM (right [x]))
 3. y←p [x]
 4. While y ≠ NIL and x = right [y]
 5. do x←y
 6. y←p[y]
 7. return y.

The code for TREE-SUCCESSOR is broken into two cases. If the right subtree of node x is nonempty, then the successor of x is just the leftmost node in the right subtree, which we find in line 2 by calling TREE-MINIMUM (right [x]). On the other hand, if the right subtree of node x is empty and x has a successor y, then y is the lowest ancestor of x whose left child is also an ancestor of x. To find y, we quickly go up the tree from x until we encounter a node that is the left child of its parent; lines 3-7 of TREE-SUCCESSOR handle this case.

The running time of TREE-SUCCESSOR on a tree of height h is O (h) since we either follow a simple path up the tree or follow a simple path down the tree. The procedure TREE-PREDECESSOR, which is symmetric to TREE-SUCCESSOR, also runs in time O (h).

4. Insertion in Binary Search Tree: To insert a new value into a binary search tree T, we use the procedure TREE-INSERT. The procedure takes a node � for which key [z] = v, left [z] NIL, and right [z] = NIL. It modifies T and some of the attributes of z in such a way that it inserts into an appropriate position in the tree.

TREE-INSERT (T, z)
 1. y ←NIL.
 2. x←root [T]
 3. while x ≠ NIL.
 4. do y←x
 5. if key [z]< key [x]
 6. then x←left [x].
 7. else x←right [x].
 8. p [z]←y
 9. if y = NIL.
 10. then root [T]←z
 11. else if key [z] < key [y]
 12. then left [y]←z

For Example: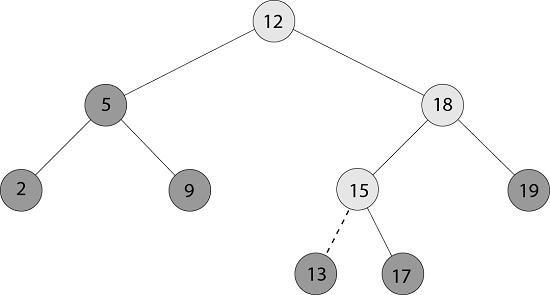

Fig: Working of TREE-INSERT

Suppose we want to insert an item with key 13 into a Binary Search Tree.

Now our node z will be either left or right child of its parent (y).

So, insert a node in the left of node index at 6.

5. Deletion in Binary Search Tree: When Deleting a node from a tree it is essential that any relationships, implicit in the tree can be maintained. The deletion of nodes from a binary search tree will be considered:

There are three distinct cases:

1. Nodes with no children: This case is trivial. Simply set the parent's pointer to the node to be deleted to nil and delete the node.
2. Nodes with one child: When z has no left child then we replace z by its right child which may or may not be NIL. And when z has no right child, then we replace z with its right child.
3. Nodes with both Childs: When z has both left and right child. We find z's successor y, which lies in right z's right subtree and has no left child (the successor of z will be a node with minimum value its right subtree and so it has no left child).
   • If y is z's right child, then we replace z.
   • Otherwise, y lies within z's right subtree but not z's right child. In this case, we first replace z by its own right child and the replace z by y.

TREE-DELETE (T, z)
 1. If left [z] = NIL or right [z] = NIL.
 2. Then y ← z
 3. Else y  ← TREE- SUCCESSOR (z)
 4. If left [y] ≠ NIL.
 5. Then x ← left [y]
 6. Else x ← right [y]
 7. If x ≠NIL
 8. Then p[x] ← p [y]
 9. If p[y] = NIL.
 10. Then root [T] ← x
 11. Else if y = left [p[y]]
 12. Then left [p[y]] ← x
 13. Else right [p[y]] ← y
 14. If y ≠ z.
 15. Then key [z] ← key [y]
 16. If y has other fields, copy them, too.
 17. Return y

The Procedure runs in O (h) time on a tree of height h.

For Example: Deleting a node z from a binary search tree. Node z may be the root, a left child of node q, or a right child of q.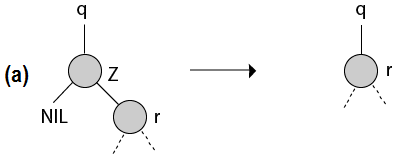

Z has the only right child.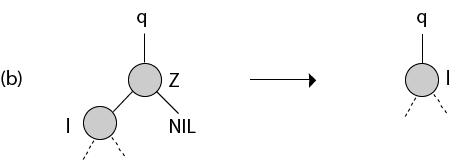

Z has the only left child. We replace z by l.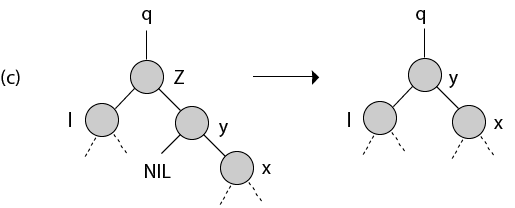

Node z has two children; its left child is node l, its right child is its successor y, and y's right child is node x. We replace z by y, updating y's left child to become l, but leaving x as y's right child.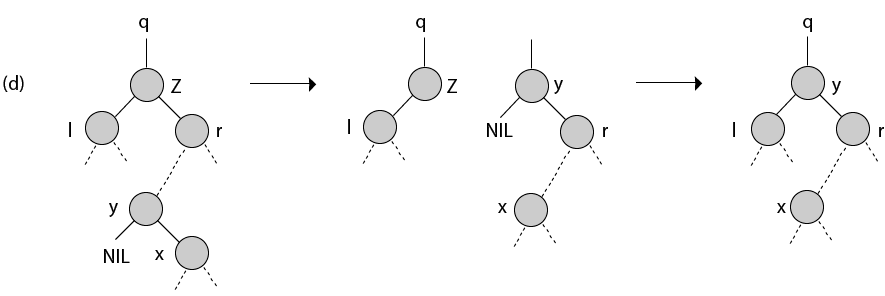

Node z has two children (left child l and right child r), and its successor y ≠ r lies within the subtree rooted at r. We replace y with its own right child x, and we set y to be r's parent. Then, we set y to be q's child and the parent of l.