Algorithm for Binary Search

Binary search is a fundamental searching algorithm used to efficiently locate a target value within a sorted array or list. It follows the principle of divide and conquers, making it highly efficient for large datasets. Binary search operates by repeatedly dividing the search space in half, narrowing down the possible locations of the target value until it is found or determined to be absent.

The algorithm begins by examining the middle element of the sorted array. If the middle element matches the target value, the search is successful, and the algorithm returns the index of the element. If the target value is less than the middle element, the algorithm recursively repeats the search process on the lower half of the array. Conversely, if the target value is greater than the middle element, the algorithm searches the upper half of the array. This process of dividing the search space in half and selecting the appropriate half for further exploration is continued until the target value is found or the search space becomes empty.

Histroy of Binary Search

In the realm of computer science, binary search stands tall as a fundamental algorithm that has revolutionized the way we search and retrieve information. It is a powerful and elegant technique that efficiently locates a target value within a sorted array. To truly appreciate its significance, we must delve into the fascinating history of binary search, tracing its roots back to ancient times.

The concept of binary search can be traced back to the work of ancient mathematicians and scholars. The idea of searching for a specific value within a sorted list has intrigued intellectuals for centuries. The great ancient Greek mathematician Euclid is often credited with formulating an early version of the binary search algorithm in the third century BCE. Euclid's algorithm, known as the "method of exhaustion," involved iteratively dividing a range in half until the desired value was found.

Fast forward to the mid-20th century, the binary search algorithm started to gain traction in the emerging field of computer science. It was during this time that pioneers like John Mauchly and J. Presper Eckert laid the foundation for electronic digital computers. As computers became more prevalent, the need for efficient search algorithms became increasingly apparent.

In 1946, a groundbreaking development took place at the Moore School of Electrical Engineering at the University of Pennsylvania. The Electronic Numerical Integrator and Computer (ENIAC), one of the world's first general-purpose electronic computers, was unveiled. ENIAC opened up new avenues for computational research, including the exploration of more sophisticated search algorithms.

It was in this context that binary search found its way into the realm of digital computing. The year 1946 marked a significant milestone with the publication of a seminal paper by John W. Mauchly and William S. Burroughs. In their paper, they described a binary search algorithm tailored specifically for electronic digital computers, which utilized the power of binary arithmetic and iterative halving to efficiently locate desired values.

The subsequent decades witnessed a steady refinement of the binary search algorithm. Computer scientists and researchers from around the world sought to improve its efficiency and adapt it to various applications. In 1962, Donald Knuth, a prominent figure in the field of computer science, introduced a binary search algorithm that is widely used to this day. Knuth's algorithm, known as the binary search with middle element, incorporated a more elegant approach that eliminated unnecessary calculations and further optimized the search process.

The advent of high-level programming languages and the proliferation of computing platforms in the latter half of the 20th century propelled binary search to even greater prominence. It became an essential tool in computer programming, allowing developers to efficiently search through vast amounts of data in a fraction of the time previously required.

In conclusion, the history of binary search is a testament to the enduring quest for efficient algorithms. From its early conceptualization by ancient mathematicians to its integration into the digital realm, binary search has evolved and matured over the centuries. Its continued relevance and widespread adoption in modern computing are a testament to its elegance and effectiveness. As we move forward into an increasingly data-driven world, the legacy of binary search will undoubtedly continue to shape the way we navigate and retrieve information efficiently.

Binary search's efficiency lies in its ability to eliminate large portions of the dataset with each iteration. By halving the search space at every step, the algorithm quickly narrows down the possible locations of the target value. This results in a time complexity of O (log n), where n represents the size of the array. The logarithmic time complexity signifies that binary search can efficiently handle even massive datasets, as the number of required comparisons grows logarithmically with the size of the input. It is important to note that binary search requires the input array to be sorted initially. If the array is not sorted, the algorithm may produce incorrect results. Additionally, binary search assumes random access to array elements, meaning that accessing the middle element can be done in constant time. This assumption is typically met in array-based data structures.

Conditions for when to apply Binary Search in a Data Structure:

To apply Binary Search algorithm:

• The data structure must be sorted.
• Access to any element of the data structure takes constant time.

Binary Search Algorithm:

• Compare the middle element of the search space with the key.
• If the key is found at middle element, the process is terminated.
• If the key is not found at middle element, choose which half will be used as the next search space.
• If the key is smaller than the middle element, then the left side is used for next search.
• If the key is larger than the middle element, then the right side is used for next search.
• This process is continued until the key is found or the total search space is exhausted.

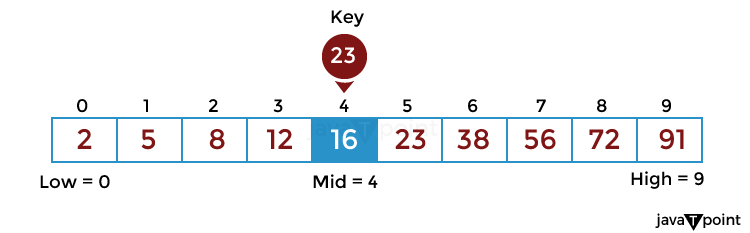
How does Binary Search work?

To understand the working of binary search, consider the following illustration:

Consider an array arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91}, and the target = 23.

First Step: Calculate the mid and compare the mid element with the key. If the key is less than mid element, move to left and if it is greater than the mid then move search space to the right.

• Key (i.e., 23) is greater than current mid element (i.e., 16). The search space moves to the right.
  
• Key is less than the current mid 56. The search space moves to the left.
  

Second Step: If the key matches the value of the mid element, the element is found and stop search.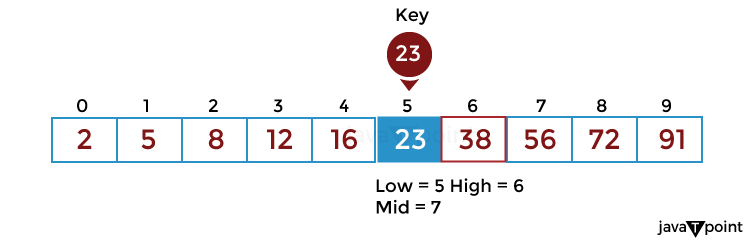

How to Implement Binary Search?

The Binary Search Algorithm can be implemented in the following two ways

• Iterative Binary Search Algorithm
• Recursive Binary Search Algorithm

Given below are the pseudo codes for the approaches.

1. Iterative Binary Search Algorithm:

Here we use a while loop to continue the process of comparing the key and splitting the search space in two halves.

Below is the example of a code in C++:

Output:

Element is present at index 3
Process executed in 1.11 seconds
Press any key to continue.

Time Complexity: O (log N)

Auxiliary Space: O (1)

2. Algorithm for Recursive Binary Search:

Make a recursive function, and compare the key's midpoint with the search space's midpoint. And depending on the outcome, either invoke the recursive procedure for the following search space or return the index where the key was discovered.

Below is the example of a program in C++:

Output:

Element is present at index 3
Process executed in 1.11 seconds
Press any key to continue.

Time Complexity:

Best Case: O(1)

Average Case: O(log N)

Worst Case: O(log N)

Auxiliary Space: O(1), If the recursive call stack is considered then the auxiliary space will be O(logN).

Complexity Analysis of Binary Search

Binary Search Algorithm Best Case Time Complexity: O(1)

The element's position at the array's middle index is ideal. The target element may be located with just one comparison. Therefore, O(1) is the best case complexity.

Average Case Time Complexity of Binary Search Algorithm: O(log N)

Worst CaseTime Complexity of Binary Search Algorithm: O(log N)

The worst case will be when the element is present in the first position. As seen in the average case, the comparison required to reach the first element is logN. So the time complexity for the worst case is O(logN).

Auxiliary Space Complexity of Binary Search Algorithm

Binary Search Algorithm uses no extra space to search the element. Hence its auxiliary space complexity is O(1)

The benefits of binary search

• Particularly for big arrays, binary search is quicker than linear search.
• More effective than other search algorithms with a comparable temporal complexity, such exponential or interpolation search.
• Large datasets kept in external memory, such a hard drive or the cloud, are best searched via binary search.

Negative aspects of binary search

• Sorting the array is necessary.
• The data structure being searched must be kept in a set of contiguous memory regions in order to use binary search.
• The array's items must be similar, which means they must be able to be sorted, in order for binary search to work.

Binary search applications:

• For more complicated machine learning algorithms, such those for training neural networks or determining a model's ideal hyper parameters, binary search can be utilized as a building block.
• It may be used to look for computer graphics-related terms like ray tracing or texture mapping algorithms.
• It may be applied to database searches.