Clique

To Prove: - Clique is an NPC or not?

For this you have to satisfy the following below-mentioned points: -

1. Clique
2. 3CNF ≤ρ Clique
3. Clique ≤ρ 3CNF≤SAT
4. Clique ϵ NP

1) Clique

Definition: - In Clique, every vertex is directly connected to another vertex, and the number of vertices in the Clique represents the Size of Clique.

CLIQUE COVER: - Given a graph G and an integer k, can we find k subsets of verticesV₁, V₂...V_K, such that UiVi = V, and that each Vi is a clique of G.

The following figure shows a graph that has a clique cover of size 3.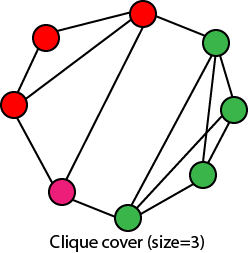

2)3CNF ≤ρ Clique

Proof:-For the successful conversion from 3CNF to Clique, you have to follow the two steps:-

Draw the clause in the form of vertices, and each vertex represents the literals of the clauses.

1. They do not complement each other
2. They don't belong to the same clause
   In the conversion, the size of the Clique and size of 3CNF must be the same, and you successfully converted 3CNF into Clique within the polynomial time

Clique ≤ρ 3CNF

Proof: - As you know that a function of K clause, there must exist a Clique of size k. It means that P variables which are from the different clauses can assign the same value (say it is 1). By using these values of all the variables of the CLIQUES, you can make the value of each clause in the function is equal to 1

Example: - You have a Boolean function in 3CNF:-

(X+Y+Z) (X+Y+Z') (X+Y'+Z)

After Reduction/Conversion from 3CNF to CLIQUE, you will get P variables such as: - x +y=1, x +z=1 and x=1

Put the value of P variables in equation (i)

(1+1+0)(1+0+0)(1+0+1)

(1)(1)(1)=1 output verified

4) Clique ϵ NP:-

Proof: - As you know very well, you can get the Clique through 3CNF and to convert the decision-based NP problem into 3CNF you have to first convert into SAT and SAT comes from NP.

So, concluded that CLIQUE belongs to NP.

Proof of NPC:-

1. Reduction achieved within the polynomial time from 3CNF to Clique
2. And verified the output after Reduction from Clique To 3CNF above
   So, concluded that, if both Reduction and verification can be done within the polynomial time that means Clique also in NPC.