Fibonacci sequence

Fibonacci sequence is the sequence of numbers in which every next item is the total of the previous two items. And each number of the Fibonacci sequence is called Fibonacci number.

Example: 0 ,1,1,2,3,5,8,13,21,....................... is a Fibonacci sequence.

The Fibonacci numbers F_nare defined as follows:

F0 = 0
Fn=1
Fn=F(n-1)+ F(n-2)

FIB (n) 
 1. If (n < 2) 
 2. then return n 
 3. else return FIB (n - 1) + FIB (n - 2)

Figure: shows four levels of recursion for the call fib (8):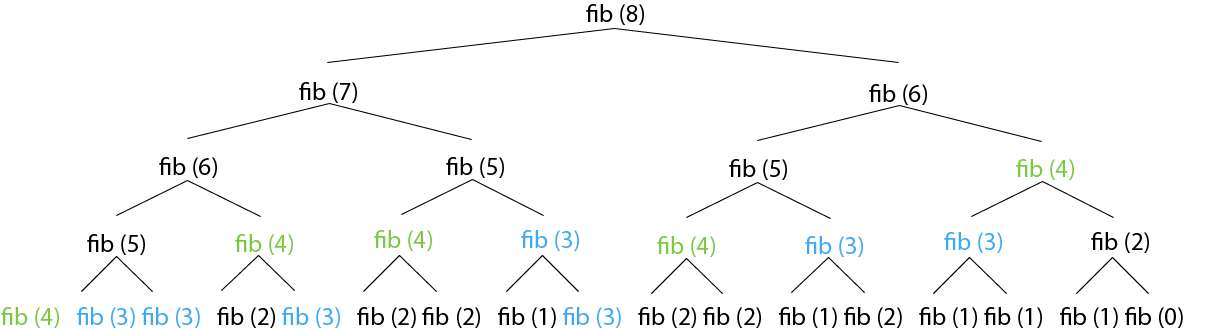

Figure: Recursive calls during computation of Fibonacci number

A single recursive call to fib (n) results in one recursive call to fib (n - 1), two recursive calls to fib (n - 2), three recursive calls to fib (n - 3), five recursive calls to fib (n - 4) and, in general, Fk-1 recursive calls to fib (n - k) We can avoid this unneeded repetition by writing down the conclusion of recursive calls and looking them up again if we need them later. This process is called memorization.

Here is the algorithm with memorization

MEMOFIB (n)
 1 if (n < 2) 
 2 then return n
 3 if (F[n] is undefined)
 4 then F[n] ← MEMOFIB (n - 1) + MEMOFIB (n - 2)
 5 return F[n]

If we trace through the recursive calls to MEMOFIB, we find that array F [] gets filled from bottom up. I.e., first F [2], then F [3], and so on, up to F[n]. We can replace recursion with a simple for-loop that just fills up the array F [] in that order

ITERFIB (n) 
 1 F [0] ← 0 
 2 F [1] ← 1 
 3 for i ← 2 to n 
 4 do 
 5 F[i] ← F [i - 1] + F [i - 2] 
 6 return F[n]

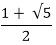This algorithm clearly takes only O (n) time to compute Fn. By contrast, the original recursive algorithm takes O (∅^n;),∅ = = 1.618. ITERFIB conclude an exponential speedup over the original recursive algorithm.