Hashing algorithm

The term "hashing" refers to the act of creating a fixed-size output from a variable-size input using a hash function. This method establishes an index or place where an item will be stored in a data structure.

Need for Hash Data Structures

The amount of data on the internet is growing exponentially every day, making it difficult to store it all effectively. Even though this amount of data may not be large in day-to-day programming, it must be conveniently saved, retrieved, and processed. The Array data structure is one of the most popular ones used for this kind of function.

Now the issue raised is why create a new data structure if Array already existed? The term "efficiency" has the solution to this. While searching in an array requires at least O(log n) time, storing in one just requires O(1) time. Although this time seems insignificant, it can really cause a lot of issues for a huge data collection, which renders the Array data structure ineffective. We are now searching for a data structure that can store the data and perform searches within it in O(1) time, or constant time. The Hashing data structure was developed in this manner. Data may now be readily stored in constant time and retrieved in constant time thanks to the invention of the Hash data structure.

Component in Hashing

Hashing primarily consists of three parts:

• Key: A key is any text or number that is provided as input into a hash function, a method for determining an item's index or placement in a data structure.
• Hash Function: The hash function takes a key as input and outputs the index of a hash table's entry. The index is sometimes referred to as a hash index.
• Hash Table: A hash table is a type of data structure that uses a unique function called a hash function to map keys to values. Hash holds the data in an array in an associative fashion, giving each data value a distinct index.

How is hashing implemented?

Let's say we want to store a collection of strings like "ab," "cd," and "efg" in a table.

We don't care about the string order in the table; our main goal is to find or update the information contained in the table rapidly in O(1) time. Hence, the supplied string set may serve as a key, and the string itself will serve as the string's value. But, how do we store the value that corresponds to the key?

Step 1: The hash value, which serves as the index of the data structure where the item will be stored, is calculated using hash functions, which are mathematical formulas.

Step 2: Next, let's give all alphabetical characters the values:

"a" = 1,

"b" = 2, etc.

Step 3: As a result, the string's numerical value is calculated by adding up all of the characters:

"ab" = 1 + 2 = 3,

"cd" = 3 + 4 = 7 ,

"efg" = 5 + 6 + 7 = 18

Step 4: Assume that we have a 7-column table to hold these strings. The sum of the characters in key mod Table size is utilized as the hash function in this case. By using sum(string) mod 7, we can determine where a string is located in an array.

Step 5: So we will then store

"ab" in 3 mod 7 = 3,

"cd" in 7 mod 7 = 0, and

"efg" in 18 mod 7 = 4.

With the aforementioned method, we can quickly locate the value that is stored at a particular position by utilizing a straightforward hash function to determine where a given text is located. Hence, using hashing to store (key, value) pairs of data in a table seems like a wonderful idea.

What does a Hash function mean?

The hash function uses mathematical formulae called hash functions to generate a mapping between a key and a value. A hash value or hash is the name given to the hash function's output. A representation of the original string of characters, the hash value is often shorter than the original.

Hash function types: Numerous hash functions employ keys that are either numeric or alphabetic. This page mainly discusses several hash functions:

• Division Technique.
• Mid Square Technique.
• Using the folding technique
• <a target="_blank" rel="noopener noreferrer nofollow" href="4.

The steps in this procedure are as follows: Select a consistent amount A method of multiplication such that 0 A.

What Makes a Good Hash Function?

A perfect hash function assigns each item to a distinct slot, and is referred to as such. The issue is that there is no methodical approach to create a perfect hash function given a random collection of things. We can create a perfect hash function provided we know the items and the collection will never change. Fortunately, even if the hash function is imperfect, we will still improve performance efficiency. By making the hash table bigger such that it can hold every conceivable value, we can create a perfect hash function. Each object will therefore have a special place. For a select few products, this strategy is workable, but it is not feasible when there are many potential outcomes.

Therefore, we may create our own hash function to do the same thing, but there are certain considerations to make when doing so.

The following characteristics a decent hash function need to possess:

• Effectively calculable- The keys should be dispersed equally throughout the tables (each table position is equally likely for each) ought to reduce collisions.
• Should have a low load factor (the ratio of the number of items in the table to its size).

Calculating a hash value with the hash function is difficult.

• O(n) time complexity
• O(1) Space Complexity

Issues with Hashing

If we take the aforementioned case as an example, the hash function that was employed was the sum of the letters; however, if we looked closely at the hash function, it became clear that the hash function generates the same hash result for various texts.

For instance, both "ab" and "ba" have the same hash value, while strings "cd" and "be" both have the same hash result. This is referred to as a collision and it causes issues with searching, insertion, deletion, and value updating.

Describe collision

Since the hashing procedure yields a tiny number for a large key, it is possible for two keys to provide the same result. When a freshly inserted key corresponds to an existing occupied slot, a collision handling technique must be used to address the problem.

How should collisions be handled?

There are primarily two ways to deal with collision:

• Separate Chaining
• Open Addressing

1. Separate Chaining

The goal is to create a linked list of records with the same hash function value that each cell of the hash table may point to. Although chaining is straightforward, extra memory outside the table is needed.

Example: Using a different chaining mechanism for collision resolution, we must enter certain entries into the hash table after receiving the hash function.

Let's look at a step-by-step solution to the aforementioned issue:

Step 1: Create an empty hash table with a potential range of hash values between 0 and 4, using the specified hash algorithm.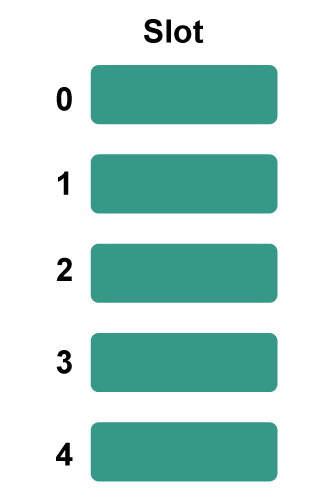

Step 2: Now add each key individually to the hash table. The hash function 12%5=2 is used to determine the bucket number 2 for the first key to be added, which are 12.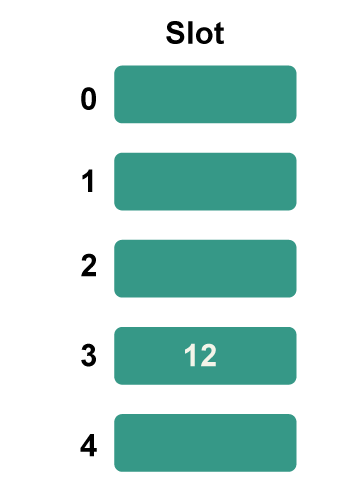

Step3: Now 22 is the current next key. Since 22%5=2, it will correspond to bucket number 2. Key 12 has already occupied bucket 2 however.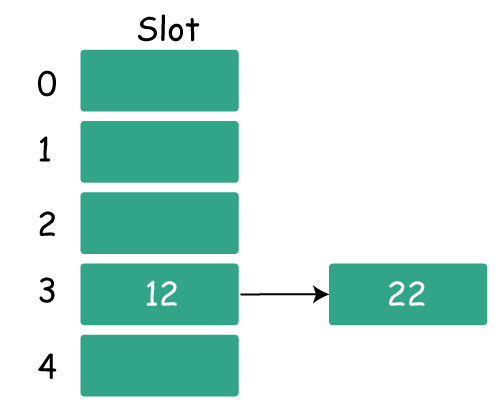

Step 4: The next key is 15. Since 15%5=0, it will map to slot number 0.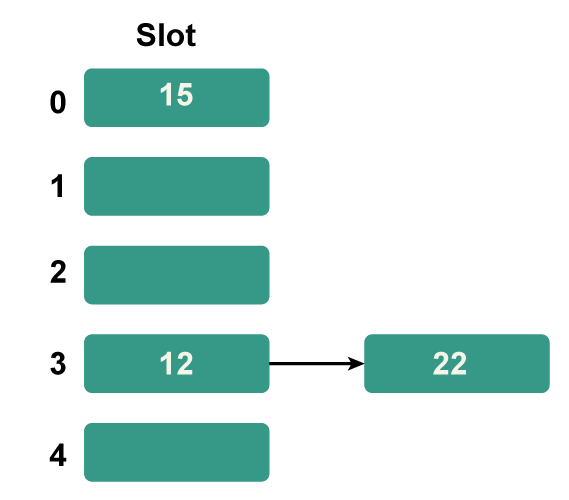

Step 5: Now 25 is the current next key. It will have a bucket number of 25%5=0. Key 25 has already occupied bucket 0 however. In order to address the collision, the separate chaining technique will once more create a linked list with bucket 0.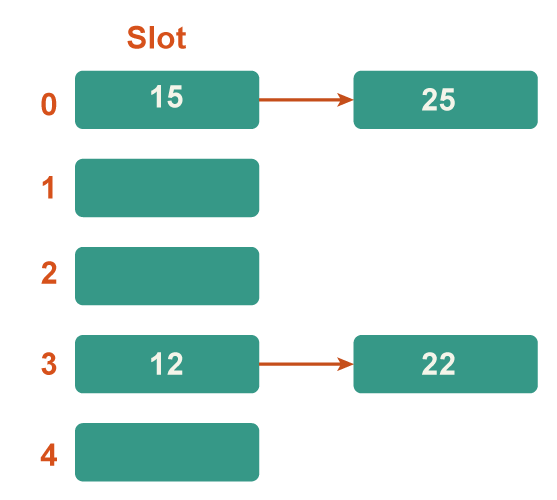

Hence In this case, the collision resolution approach is the separate chaining method.

2. Open Addressing

In open addressing, the hash table alone houses all of the components. Either a record or NIL is present in every table entry. When looking for an element, we go through each table slot individually until the sought-after element is discovered or it becomes obvious that the element is not in the table.

a) Linear Probing

In linear probing, the hash table is systematically examined beginning at the hash's initial point. If the site we get is already occupied, we look for a different one.

Algorithm:

• Calculate the hash key. i.e. key = data % size
• Check, if hashTable[key] is empty store the value directly by hashTable[key] = data
• If the hash index already has some value then check for next index using key = (key+1) % size
• Check, if the next index is available hashTable[key] then store the value. Otherwise try for next index.
• Do the above process till we find the space.

Example: Consider the following basic hash function, "key mod 5", with the following keys to be inserted: 50, 70, 76, 85, and 93.

Step 1: First, create an empty hash table with a potential range of hash values between 0 and 4, using the specified hash algorithm.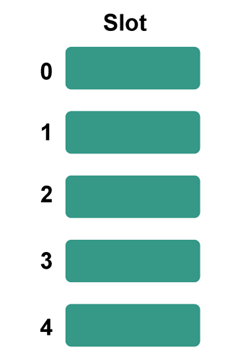

Step 2: Now add each key individually to the hash table. 50 is the first key. Because 50%5=0, it will map to slot number 0. Therefore, place it in slot number 0.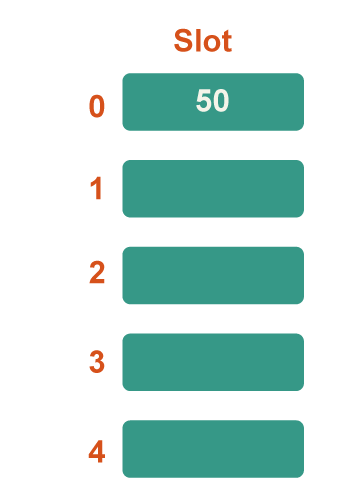

Step 3: Now 70 is the next key. Since 50 is already in slot number 0, it will map to slot number 0 since 70%5=0, therefore look for the next vacant slot and place it there.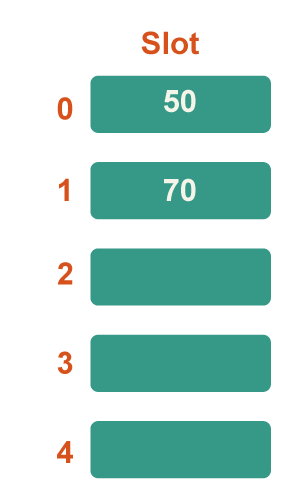

Step 4: Now 76 is the next key. Because 76%5=1, it will map to slot number 1, but because slot number 1 is already occupied by 70, find the following vacant slot and insert it.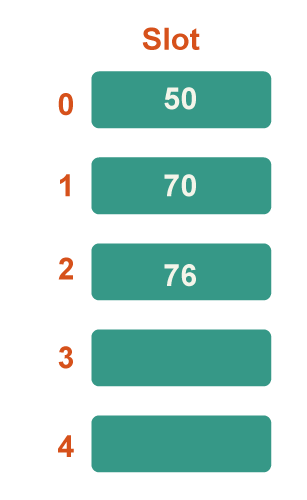

Step 5: Now 93 is the next key. Because 93%5=3, it will map to slot number 3, so put it there.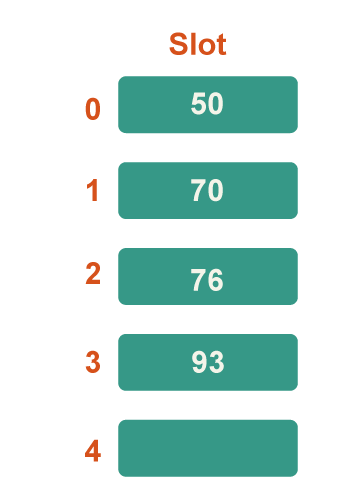

b) Quadratic Probing

In computer programming, quadratic probing is an open addressing approach for resolving hash collisions in hash tables. Until an available slot is discovered, quadratic probing works by adding consecutive values of any arbitrary quadratic polynomial to the initial hash index.

This technique is often referred to as the "mid-square method" because it searches for the i2'th probe (slot) in the i²th iteration with i = 0, 1,... n - 1. We always begin where the hash was generated. We examine the other slots if just the location is taken.

Let n be the size of the hash table and let hash(x) be the slot index determined by the hash algorithm.

Example: Consider the following example table: Size = 7, Hash(x) = x% 7, and Collision Resolution Strategy: f(i) = i². Add 22, 30, and 50.

Step 1: Create a table of size 7.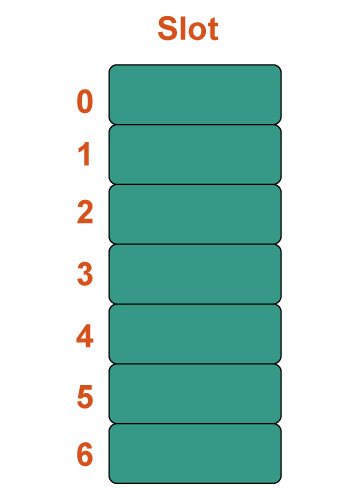

Step 2: Add 22 and 30.

Hash(25) = 22 % 7 = 1, We can simply put 22 at slot 1 because the cell at index 1 is vacant.

Hash(30) = 30 % 7 = 2, We can simply put 30 at slot 2 because the cell at index 2 is vacant.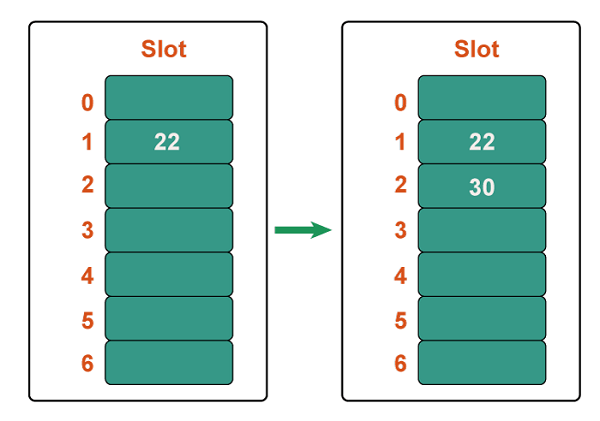

Step 3: Inserting 50

Hash(25) = 50 % 7 = 1

In our hash table slot 1 is already occupied. So, we will search for slot 1+12, i.e. 1+1 = 2,

Again slot 2 is found occupied, so we will search for cell 1+22, i.e.1+4 = 5, Now, cell 5 is not occupied so we will place 50 in slot 5.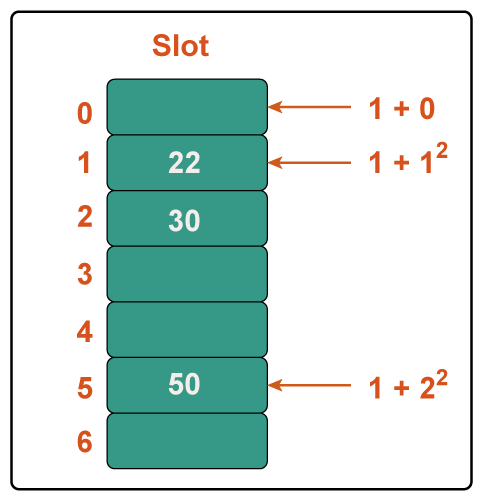

What does "load factor" in hashing mean?

The number of entries in the hash table divided by the size of the hash table is known as the load factor of the hash table. When we want to rehash a prior hash function or want to add more entries to an existing hash table, the load factor is the key parameter that we employ.

It aids in evaluating the effectiveness of the hash function by indicating whether or not the keys are distributed evenly throughout the hash table when we use that particular hash algorithm.

Complexity and Load Factor

• The K and the hash function determine how long the first step will take. The length of the string may affect the hash function, for instance, if the key is the string "abcd". However, for extremely high values of n, the number of map entries and the length of the keys are virtually insignificant in proportion to n, therefore hash calculation may be thought of as occurring in constant time, i.e., O(1).
• The list of K-V pairings that are present at that index must be traversed for the second step. The worst scenario in this circumstance may be that all n items are located at the same index. So, O (n) would be the temporal complexity. However, enough work has been done to ensure that hash algorithms evenly divide the array's keys, so this hardly ever occurs.
• Accordingly, there would be n/b items on each index if there are n entries and b is the array's size. The load factor, or n/b, is the number that indicates the load on our map.
• This load factor must be kept low in order to reduce the amount of entries in a single index and maintain a nearly constant complexity, i.e., O (1).

What does Rehashing mean?

Rehashing, as the name implies, entails hashing once again. In essence, the complexity grows as the load factor rises over its initial value (the load factor is 0.75 by default). In order to maintain a low load factor and minimal complexity, the array's size is expanded (doubled), and all of the values are hashed again and saved in the new double-sized array.

The load factor (i.e., the proportion of the number of items to the number of buckets) rises when a hash map fills up. Performance issues may result from an increase in accidents as the load factor rises. This may be avoided by resizing the hashmap and rehashing the elements to new buckets, which lowers the load factor and lowers the likelihood of collisions.

Each element of the hash map is iterated during rehashing, and the new bucket locations for each element are determined using the new hash function that is appropriate for the changed hash map size. Although this procedure might take a while, it is vital to keep the hash map functioning well.

Why rehashing?

In order to avoid collisions and keep the data structure's efficiency, rehashing is required.

The load factor (i.e., the ratio of the number of items to the number of buckets) rises when elements are added to a hash map. The hash map loses efficiency as more collisions occur as the load factor rises over a certain threshold, which is often set at 0.75. This may be avoided by resizing the hash map and rehashing the elements to new buckets, which lowers the load factor and lowers the likelihood of collisions. This method is called rehashing.

Rehashing can be expensive in terms of both time and space, but it is important to preserve the hash map's effectiveness.

How does rehashing work?

Following are some examples of rehashing:

• Check the load factor once each new entry is added to the map.
• Rehash if it exceeds the pre-defined value (or, if none is provided, the default value of 0.75).
• Create a new bucket array for Rehash that is twice as large as the old one.
• After that, go through the old bucket array element by element and use insert () for each one to add it to the new, larger bucket array.

Uses for the hash data structure

• Databases employ hash for indexing.
• Disk-based data structures employ hash.
• JavaScript hash is used to implement objects in various computer languages, such as Python.

Hash data structure applications in real time

• Cache mapping uses hash for quick access to the data.
• Password verification may be done using hashes.
• As a message digest in cryptography, hash is utilized.
• For matching patterns in a string, use the Rabin-Karp method.
• Figuring out how many distinct substrings a string has.

Hash Data Structure Benefits

• Comparatively to other data structures, hash offers greater synchronization.
• Compared to search trees or other data structures, hash tables are more effective.
• On average, hash offers constant speed for activities like searching, insertion, and deleting.

Hash Data Structure Cons

• When there are plenty of collisions, hash is wasteful.
• For a large collection of potential keys, hash collisions are essentially impossible to avoid.
• Null values are not permitted in hash.

Now let us see an example of hashing data structure:

Non-overlapping sum of two sets

Statement: Given two arrays A[] and B[] of size n. It is given that both arrays individually contain distinct elements. We need to find the sum of all elements that are not common.

For Example:

Brute Force Method: One straightforward method is to first check to see if each element in A[] is also present in B[], and then, if it is, just add it to the result. In a same manner, traverse B[] and add each element that is absent from B to the result.

Time Complexity: O (n²)

Auxiliary Space: O(1), As additional space is consumed continuously.

Using the hashing idea, fill in the empty hash with the contents of the two arrays. Now, go through the hash table and add each member whose count is 1. (According to the query, each array's items are separate.)

Below is the solution of the above approach in C++:

Output

35
...........
Process executed in 0.11 seconds
Press any key to continue.

Explanation

Due to the amortized constant nature of adding an unordered map, the time complexity is O (n) and space complexity would be O(n).

Using set data structures is another strategy:

• Add Array A's items to the set data structure and total them.
• Determine if B's elements are present in the set; if so, delete the current element from the set; otherwise, add the current element to the total.
• Finally, provide the total

Below is the program in C++ for the better approach of the problem:

Output

35
........
Process executed in 0.05 seconds
Press any key to continue.

Conclusion

The purpose of hashing, according to the description above, is to address the problem of rapidly locating an item in a collection. For instance, we would use hashing to more effectively discover and find a certain keyword if we had a list of millions of English terms and wanted to find it. To search through all of the millions of listings until we discover a match would be inefficient. By limiting the search to a smaller set of terms at the start, hashing speeds up the search process.