HashingHashing is the transformation of a string of character into a usually shorter fixed-length value or key that represents the original string. Hashing is used to index and retrieve items in a database because it is faster to find the item using the shortest hashed key than to find it using the original value. It is also used in many encryption algorithms. A hash code is generated by using a key, which is a unique value. Hashing is a technique in which given key field value is converted into the address of storage location of the record by applying the same operation on it. The advantage of hashing is that allows the execution time of basic operation to remain constant even for the larger side. Why we need Hashing?Suppose we have 50 employees, and we have to give 4 digit key to each employee (as for security), and we want after entering a key, direct user map to a particular position where data is stored. If we give the location number according to 4 digits, we will have to reserve 0000 to 9999 addresses because anybody can use anyone as a key. There is a lot of wastage. In order to solve this problem, we use hashing which will produce a smaller value of the index of the hash table corresponding to the key of the user. Universal HashingLet H be a finite collection of hash functions that map a given universe U of keys into the range {0, 1..... m-1}. Such a collection is said to be universal if for each pair of distinct keys k,l∈U, the number of hash functions h∈ H for which h(k)= h(l) is at most |H|/m. In other words, with a hash function randomly chosen from H, the chance of a collision between distinct keys k and l is no more than the chance 1/m of a collision if h(k) and h(l)were randomly and independently chosen from the set {0,1,...m-1}. RehashingIf any stage the hash table becomes nearly full, the running time for the operations of will start taking too much time, insert operation may fail in such situation, the best possible solution is as follows:
Example: Consider inserting the keys 10, 22, 31,4,15,28,17,88 and 59 into a hash table of length m = 11 using open addressing with the primary hash function h' (k) = k mod m .Illustrate the result of inserting these keys using linear probing, using quadratic probing with c1=1 and c2=3, and using double hashing with h2(k) = 1 + (k mod (m-1)). Solution: Using Linear Probing the final state of hash table would be: 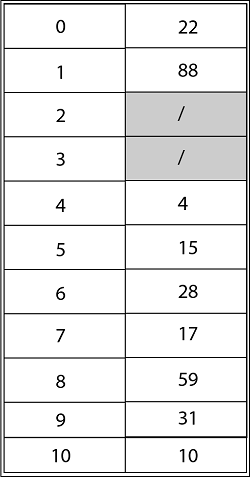
Using Quadratic Probing with c1=1, c2=3, the final state of hash table would be h (k, i) = (h' (k) +c1*i+ c2 *i2) mod m where m=11 and h' (k) = k mod m. 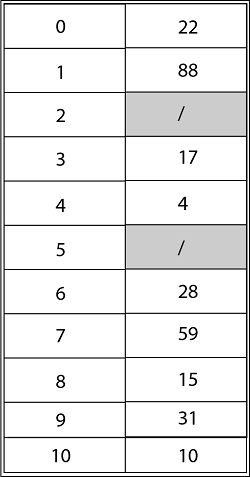
Using Double Hashing, the final state of the hash table would be: 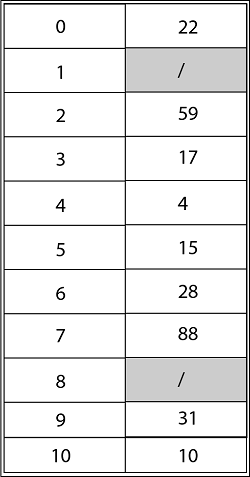
Next TopicHash Tables
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









