DAA Bubble Sort

Bubble Sort, also known as Exchange Sort, is a simple sorting algorithm. It works by repeatedly stepping throughout the list to be sorted, comparing two items at a time and swapping them if they are in the wrong order. The pass through the list is duplicated until no swaps are desired, which means the list is sorted.

This is the easiest method among all sorting algorithms.

Algorithm

Step 1 ➤ Initialization

Step 2 ➤ loop,

Step 3 ➤ comparison, loop.

Step 4 ➤ Finish, or reduce the size.

How Bubble Sort Works

1. The bubble sort starts with the very first index and makes it a bubble element. Then it compares the bubble element, which is currently our first index element, with the next element. If the bubble element is greater and the second element is smaller, then both of them will swap.
   After swapping, the second element will become the bubble element. Now we will compare the second element with the third as we did in the earlier step and swap them if required. The same process is followed until the last element.
2. We will follow the same process for the rest of the iterations. After each of the iteration, we will notice that the largest element present in the unsorted array has reached the last index.

For each iteration, the bubble sort will compare up to the last unsorted element.

Once all the elements get sorted in the ascending order, the algorithm will get terminated.

Consider the following example of an unsorted array that we will sort with the help of the Bubble Sort algorithm.

Initially,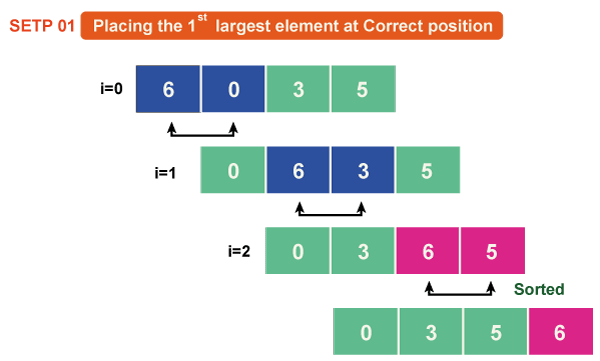

Pass 1:

• Compare a₀ and a₁

As a₀ < a₁ so the array will remain as it is.

• Compare a₁ and a₂

Now a₁ > a₂, so we will swap both of them.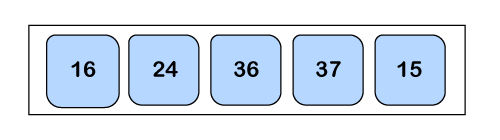

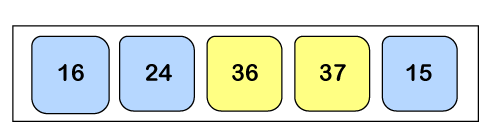
• Compare a₂ and a₃

As a₂ < a₃ so the array will remain as it is.

• Compare a₃ and a₄

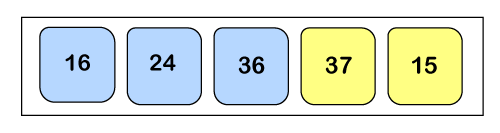
Here a₃ > a₄, so we will again swap both of them.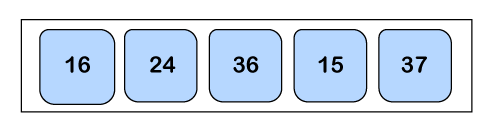

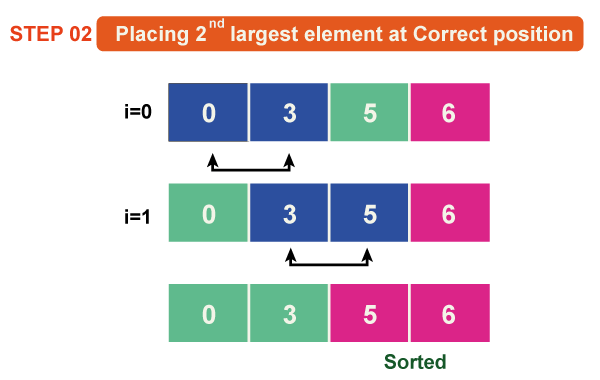
Pass 2:

• Compare a₀ and a₁

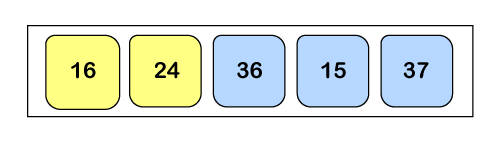
As a₀ < a₁ so the array will remain as it is.

• Compare a₁ and a₂

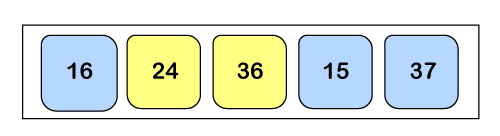
Here a₁ < a₂, so the array will remain as it is.

• Compare a₂ and a₃

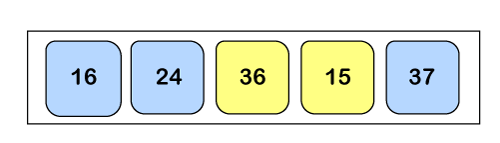
In this case, a₂ > a₃, so both of them will get swapped.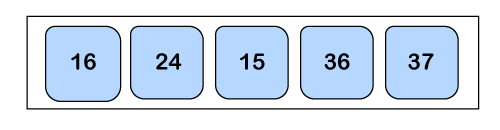

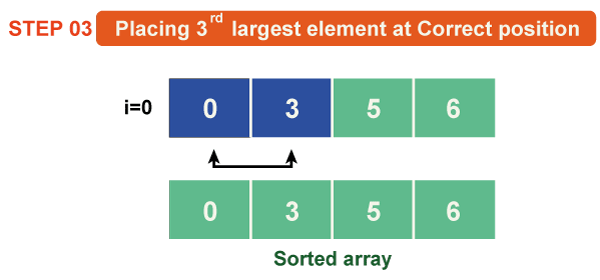
Pass 3:

• Compare a₀ and a₁

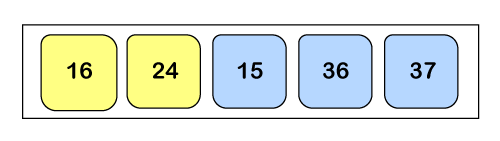
As a₀ < a₁ so the array will remain as it is.

• Compare a₁ and a₂

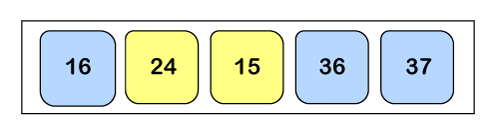
Now a₁ > a_2, so both of them will get swapped.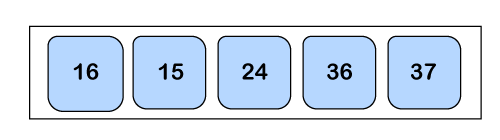

Pass 4:

• Compare a₀ and a₁

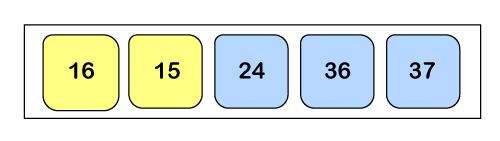
Here a₀ > a₁, so we will swap both of them.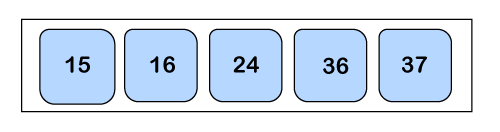

Hence the array is sorted as no more swapping is required.

Complexity Analysis of Bubble Sort

Input: Given n input elements.

Output: Number of steps incurred to sort a list.

Logic: If we are given n elements, then in the first pass, it will do n-1 comparisons; in the second pass, it will do n-2; in the third pass, it will do n-3 and so on. Thus, the total number of comparisons can be found by;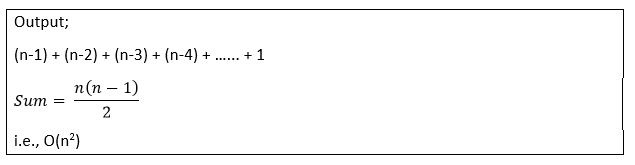

Therefore, the bubble sort algorithm encompasses a time complexity of O(n²) and a space complexity of O(1) because it necessitates some extra memory space for temp variable for swapping.

Time Complexities:

• Best Case Complexity: The bubble sort algorithm has a best-case time complexity of O(n) for the already sorted array.
• Average Case Complexity: The average-case time complexity for the bubble sort algorithm is O(n²), which happens when 2 or more elements are in jumbled, i.e., neither in the ascending order nor in the descending order.
• Worst Case Complexity: The worst-case time complexity is also O(n²), which occurs when we sort the descending order of an array into the ascending order.

Advantages of Bubble Sort

1. Easily understandable.
2. Does not necessitates any extra memory.
3. The code can be written easily for this algorithm.
4. Minimal space requirement than that of other sorting algorithms.

Disadvantages of Bubble Sort

1. It does not work well when we have large unsorted lists, and it necessitates more resources that end up taking so much of time.
2. It is only meant for academic purposes, not for practical implementations.
3. It involves the n² order of steps to sort an algorithm.