Counting Sort

It is a linear time sorting algorithm which works faster by not making a comparison. It assumes that the number to be sorted is in range 1 to k where k is small.

Basic idea is to determine the "rank" of each number in the final sorted array.

Counting Sort uses three arrays:

1. A [1, n] holds initial input.
2. B [1, n] holds sorted output.
3. C [1, k] is the array of integer. C [x] is the rank of x in A where x ∈ [1, k]

Firstly C [x] to be a number of elements of A [j] that is equal to x

• Initialize C to zero
• For each j from 1 to n increment C [A[j]] by 1

We set B[C [x]] =A[j]

If there are duplicates, we decrement C [i] after copying.

Explanation:

Step1: for loop initialize the array R to 'o'. But there is a contradict in the first step initialize of loop variable 1 to k or 0 to k. As 0&1 are based on the minimum value comes in array A (input array). Basically, we start I with the value which is minimum in input array 'A'

For loops of steps 3 to 4 inspects each input element. If the value of an input element is 'i', we increment C [i]. Thus, after step 5, C [i] holds the number of input element equal to I for each integer i=0, 1, 2.....k

Step 6 to 8 for loop determines for each i=0, 1.....how many input elements are less than or equal to i

For loop of step 9 to 11 place each element A [j] into its correct sorted position in the output array B. for each A [j],the value C [A[j]] is the correct final position of A [j] in the output array B, since there are C [A[j]] element less than or equal to A [i].

Because element might not be distinct, so we decrement C[A[j] each time we place a value A [j] into array B decrement C[A[j] causes the next input element with a value equal to A [j], to go to the position immediately before A [j] in the output array.

Analysis of Running Time:

• For a loop of step 1 to 2 take θ(k) times
• For a loop of step 3 to 4 take θ(n) times
• For a loop of step 6 to 7 take θ(k) times
• For a loop of step 9 to 11 take θ(n) times

Overall time is θ(k+n) time.

Note:

1. Counting Sort has the important property that it is stable: numbers with the same value appears in the output array in the same order as they do in the input array.
2. Counting Sort is used as a subroutine in Radix Sort.

Example: Illustration the operation of Counting Sort in the array.

Solution: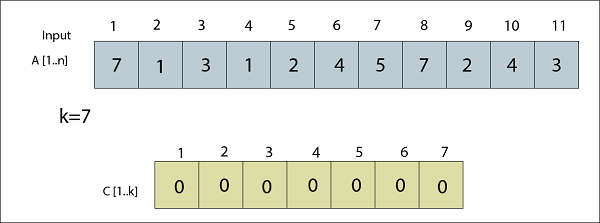

Fig: Initial A and C Arrays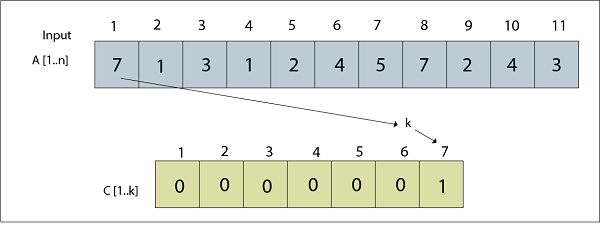

Fig: A [1] = 7 Processed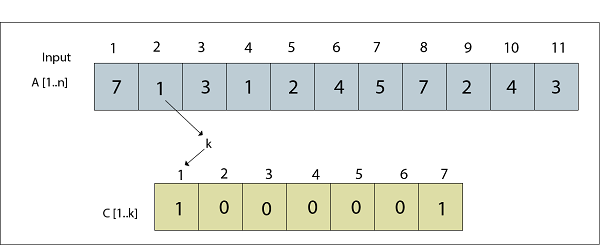

Fig: A [2] = 1 Processed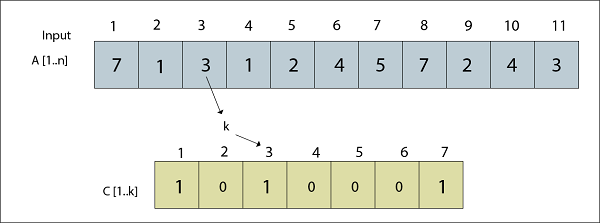

Fig: A [3] = 3 Processed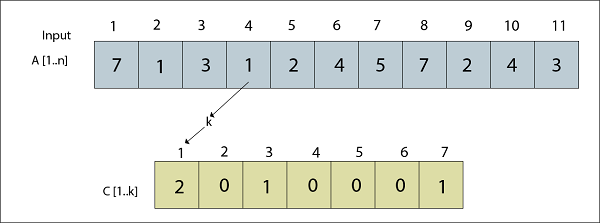

Fig: A [4] = 1 Processed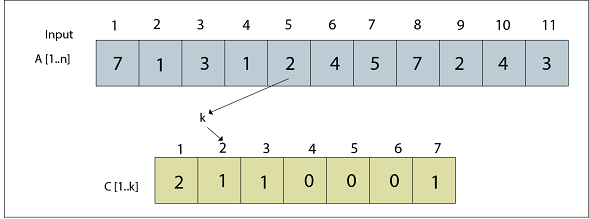

Fig: A [5] = 2 Processed

UPDATED C is: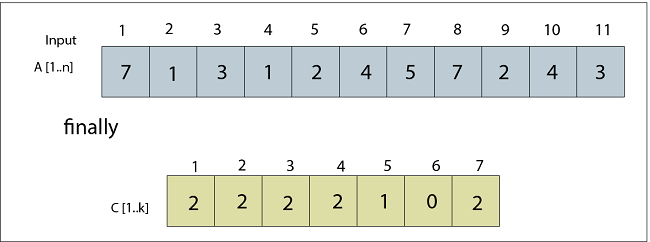

Fig: C now contains a count of elements of A

Note: here the item of 'A' one by one get scanned and will become a position in 'C' and how many times the item get accessed will be mentioned in an item in 'C' Array and it gets updated or counter increased by 1 if any item gets accessed again.

Now, the for loop i= 2 to 7 will be executed having statement:

By applying these conditions we will get C updated as i stated from 2 up to 7

C [2] = C [2] + C [1]      C [3] = C [3] + C [2]
C [2] = 2 + 2              C [3] = 2 + 4
C [2] = 4                  C [3] = 6

C [4] = C [4] + C [3]	   C [5] = C [5] + C [4]
C [4] = 2 + 6              C [5] = 1 +8
C [4] = 8                  C [5] = 9

C [6] = C [6] + C [5]      C [7] = C [7] + C [6]
C [6] = 0 + 9              C [7] = 2 + 9
C [6] = 9                  C [7] = 11

Thus the Updated C is: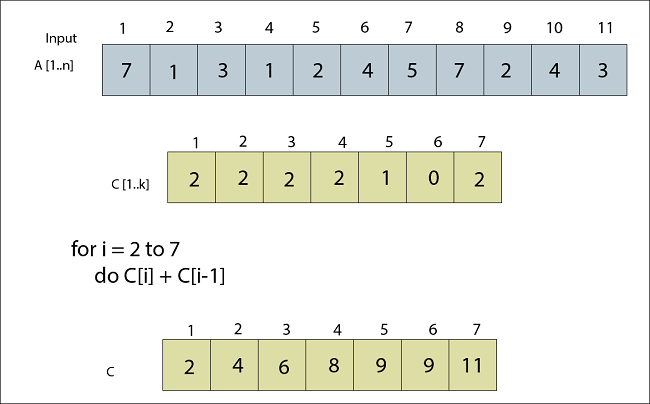

Fig: C set to rank each number of A

Now, we will find the new array B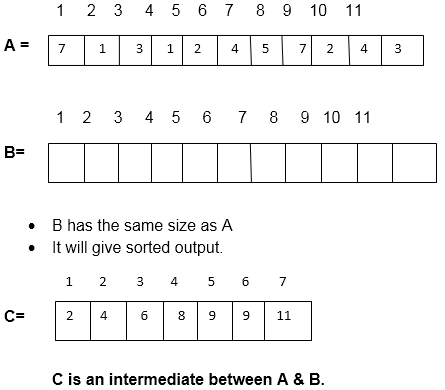

Now two Conditions will apply:

1. B[C[A[j] ← A [j]
2. C[A[j] ← C[A[j]-1

We decrease counter one by one by '1'
We start scanning of the element in A from the last position.
Element in A became a position in C

Step 1

B [C [A [11]]] = A [11]     C [A [11] = C [A [11]-1
B [C [3] = 3                C [3] = C [3] -1
B [6] = 3                   C [3] = 5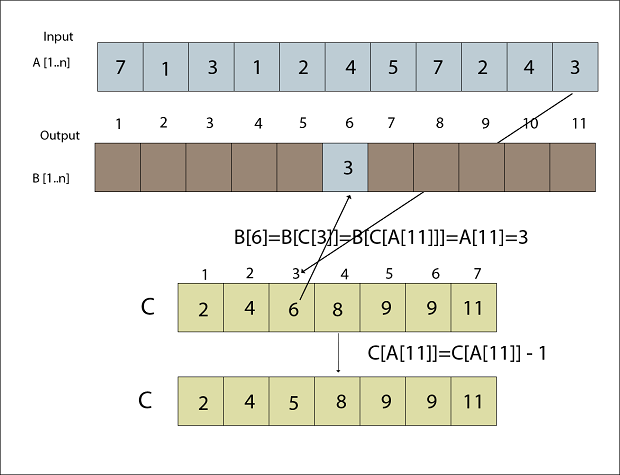

Fig: A [11] placed in Output array B

Step 2

B [C [A [10]]] = A [10]     C [A [10]] = C [A [10]]-1
B [C [4]] =4                C [4] = C [4] -1
B [8] = 4                   C [4] = 7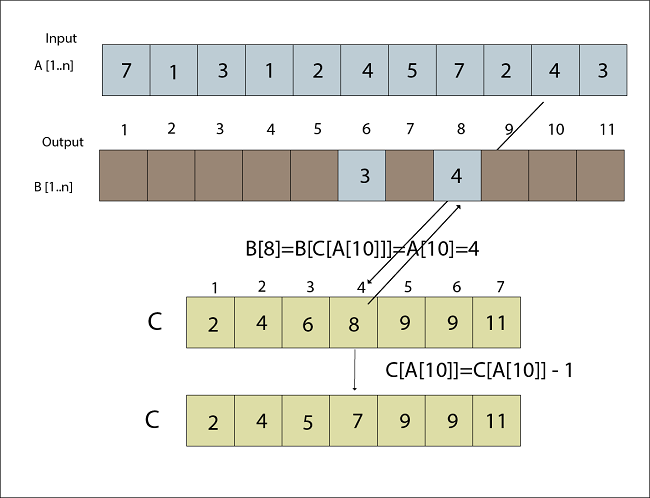

Fig: A [10] placed in Output array B

Step 3

B [C [A [9]] = A [9]        C [A [9] = C [A [9]]-1
B [C [2]] = A [2]           C [2] = C [2]-1
B [4] = 2                   C [2] = 3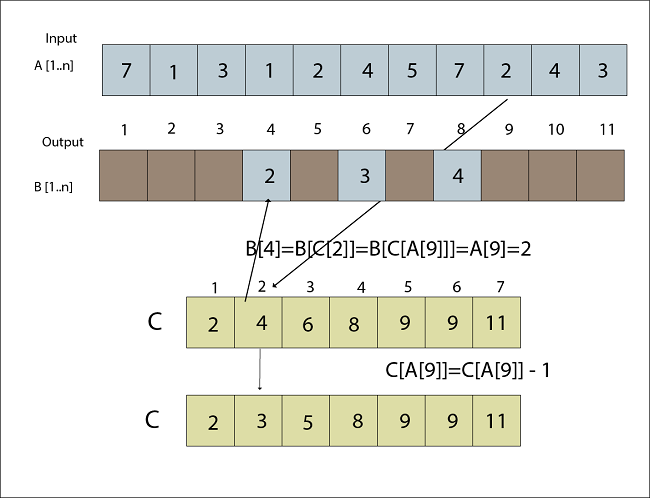

Fig: A [9] placed in Output array B

Step 4

B [C [A [8]]] = A [8]       C [A [8]] =C [A [8]] -1 
B [C [7]] =7                C [A [8]] = C [7]-1
B [11] =7                   C [7] = 10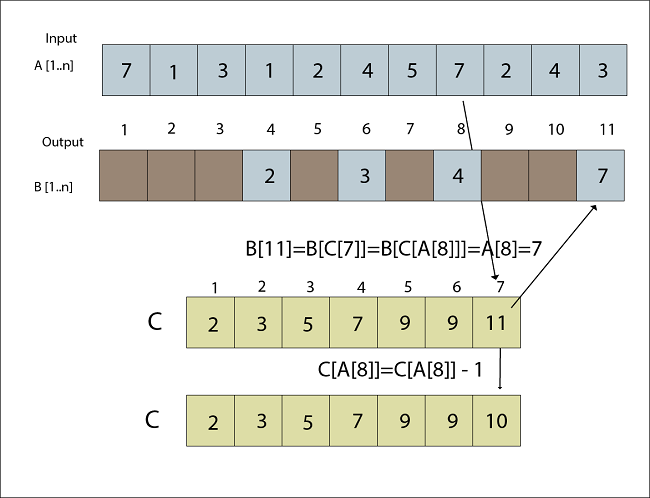

Fig: A [8] placed in Output array B

Step 5

B [C [A [7]]] = A [7]       C [A [7]] = C [A [7]] - 1 
B [C [5]] = 5               C [5] = C [5] - 1
B [9] = 5                   C [5] =8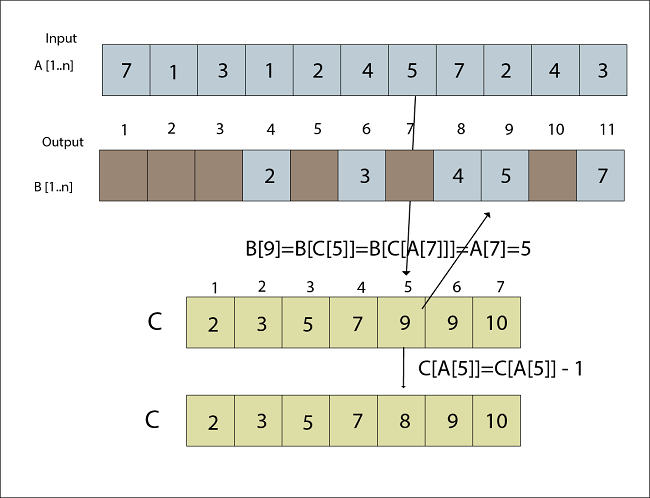

Fig: A [7] placed in Output array B

Step 6

B [C [A [6]]] = A [6]       C [A [6]] = C [A [6]] - 1
B [C [4]] = 4               C [4] = C [4] - 1
B [7] = 4                   C [4] = 6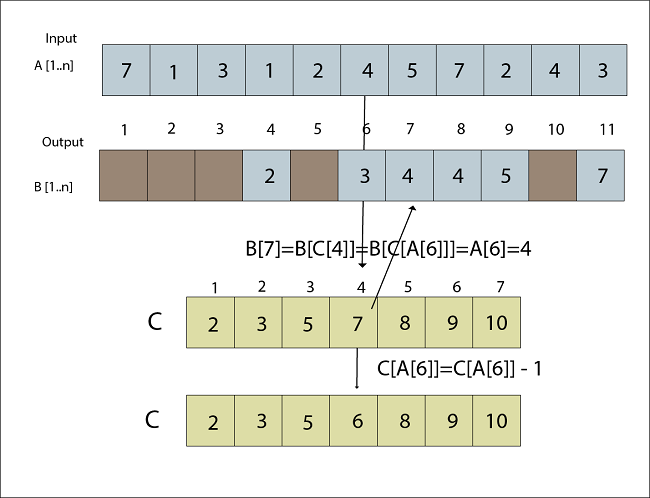

Fig: A [6] placed in Output array B

Step 7

B [C [A [5]]] = A [5]       C [A [5] = C [A [5]] -1
B [C [2] =2                 C [2] = C [2] - 1
B [3] = 2                   C [2] = 2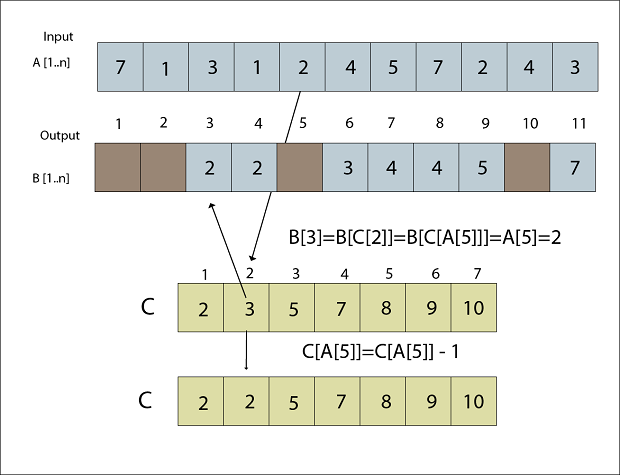

Fig: A [5] placed in Output array B

Step 8

B [C [A [4]]] = A [4]       C [A [4]] = C [A [4]] - 1
B [C [1] = 1                C [1] = C [1] - 1
B [2] = 1                   C [1] = 1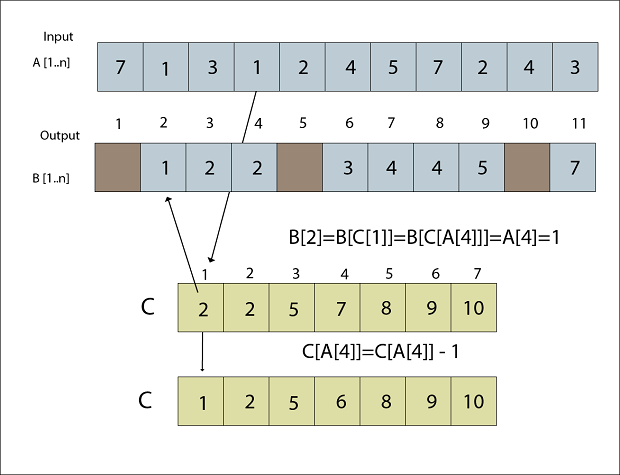

Fig: A [4] placed in Output array B

Step 9

B [C [A [3]]] = A [3]       C [A [3]] = C [A [3]] - 1
B [C [3] = 3                C [3] = C [3] - 1
B [5] = 3                   C [3] = 4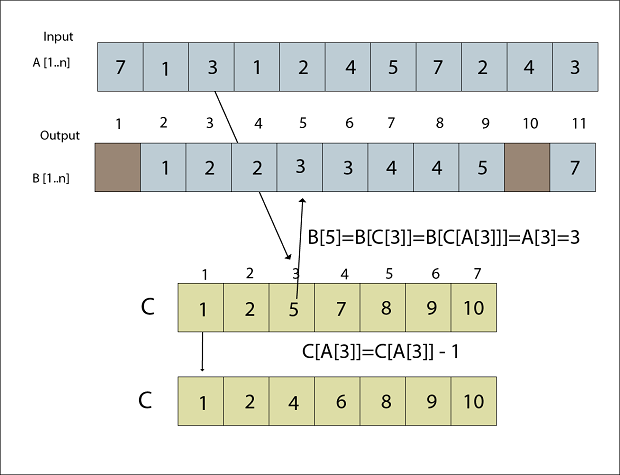

Fig: A [3] placed in Output array B

Step 10

B [C [A [2]]] = A [2]       C [A [2]] = C [A [2]] - 1
B [C [1]] = 1               C [1] = C [1] - 1	
B [1] = 1                   C [1] = 0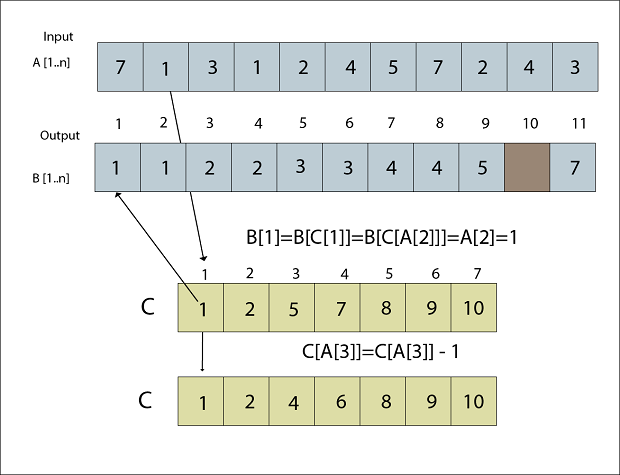

Fig: A [2] placed in Output array B

Step 11

B [C [A [1]]] = A [1]       C [A [1]] = C [A [1]] - 1
B [C [7]] = 7               C [7] = C [7] - 1
B [10] = 7                  C [7] = 9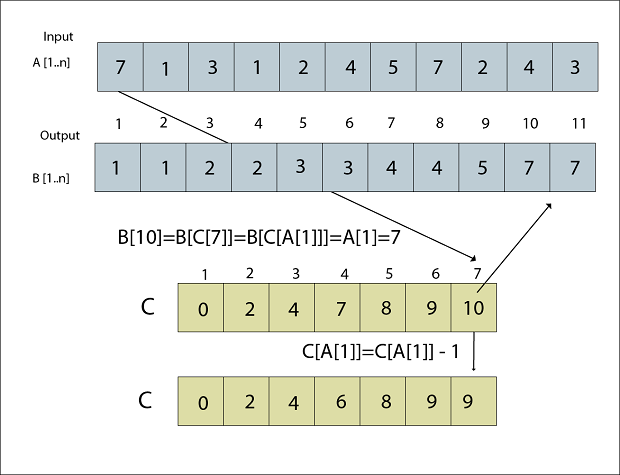

Fig: B now contains the final sorted data.