N-Queens Problem

N - Queens problem is to place n - queens in such a manner on an n x n chessboard that no queens attack each other by being in the same row, column or diagonal.

It can be seen that for n =1, the problem has a trivial solution, and no solution exists for n =2 and n =3. So first we will consider the 4 queens problem and then generate it to n - queens problem.

Given a 4 x 4 chessboard and number the rows and column of the chessboard 1 through 4.

Since, we have to place 4 queens such as q₁ q₂ q₃ and q₄ on the chessboard, such that no two queens attack each other. In such a conditional each queen must be placed on a different row, i.e., we put queen "i" on row "i."

Now, we place queen q₁ in the very first acceptable position (1, 1). Next, we put queen q₂ so that both these queens do not attack each other. We find that if we place q₂ in column 1 and 2, then the dead end is encountered. Thus the first acceptable position for q₂ in column 3, i.e. (2, 3) but then no position is left for placing queen 'q₃' safely. So we backtrack one step and place the queen 'q₂' in (2, 4), the next best possible solution. Then we obtain the position for placing 'q₃' which is (3, 2). But later this position also leads to a dead end, and no place is found where 'q₄' can be placed safely. Then we have to backtrack till 'q₁' and place it to (1, 2) and then all other queens are placed safely by moving q₂ to (2, 4), q₃ to (3, 1) and q₄ to (4, 3). That is, we get the solution (2, 4, 1, 3). This is one possible solution for the 4-queens problem. For another possible solution, the whole method is repeated for all partial solutions. The other solutions for 4 - queens problems is (3, 1, 4, 2) i.e.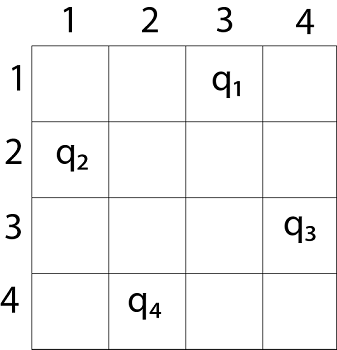

The implicit tree for 4 - queen problem for a solution (2, 4, 1, 3) is as follows: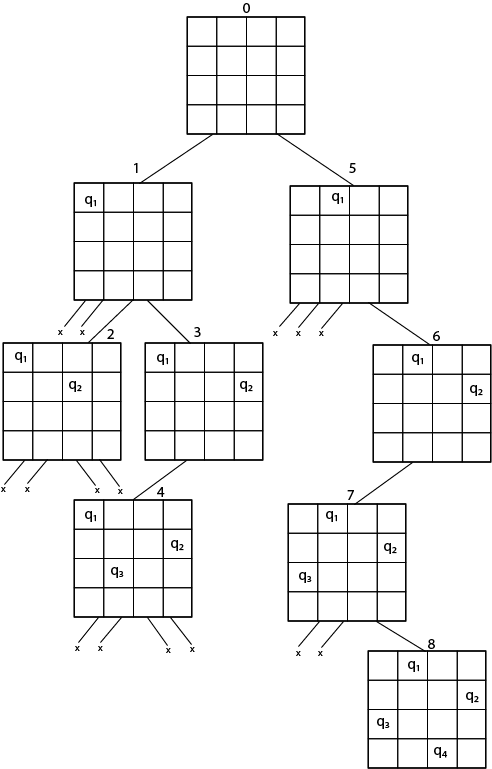

Fig shows the complete state space for 4 - queens problem. But we can use backtracking method to generate the necessary node and stop if the next node violates the rule, i.e., if two queens are attacking.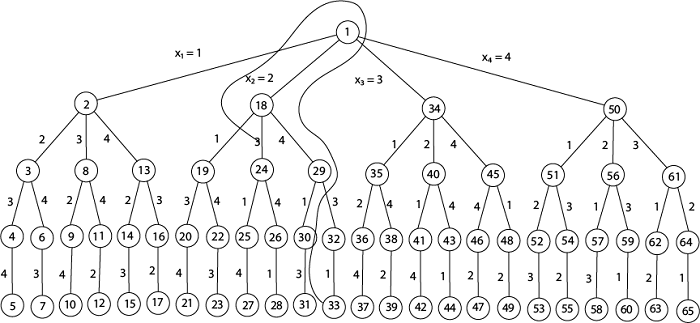

4 - Queens solution space with nodes numbered in DFS

It can be seen that all the solutions to the 4 queens problem can be represented as 4 - tuples (x₁, x₂, x₃, x₄) where x_i represents the column on which queen "q_i" is placed.

One possible solution for 8 queens problem is shown in fig: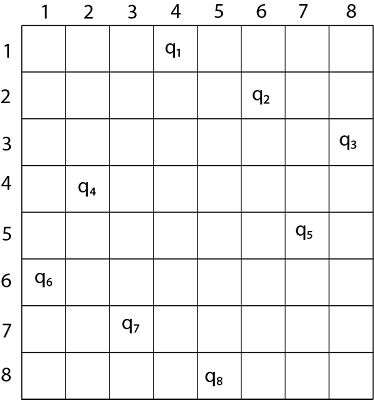

Place (k, i) returns a Boolean value that is true if the kth queen can be placed in column i. It tests both whether i is distinct from all previous costs x₁, x₂,....x_k-1 and whether there is no other queen on the same diagonal.

Using place, we give a precise solution to then n- queens problem.

Place (k, i) return true if a queen can be placed in the kth row and ith column otherwise return is false.

x [] is a global array whose final k - 1 values have been set. Abs (r) returns the absolute value of r.