Bucket Sort

Bucket Sort runs in linear time on average. Like Counting Sort, bucket Sort is fast because it considers something about the input. Bucket Sort considers that the input is generated by a random process that distributes elements uniformly over the intervalμ=[0,1].

1. Partition μ into n non-overlapping intervals called buckets.
2. Puts each input number into its buckets
3. Sort each bucket using a simple algorithm, e.g. Insertion Sort and then
4. Concatenates the sorted lists.

Bucket Sort considers that the input is an n element array A and that each element A [i] in the array satisfies 0≤A [i] <1. The code depends upon an auxiliary array B [0....n-1] of linked lists (buckets) and considers that there is a mechanism for maintaining such lists.

BUCKET-SORT (A)
 1. n ← length [A]
 2. for i ← 1 to n
 3. do insert A [i] into list B [n A[i]]
 4. for i ← 0 to n-1
 5. do sort list B [i] with insertion sort.
 6. Concatenate the lists B [0], B [1] ...B [n-1] together in order.

Example: Illustrate the operation of BUCKET-SORT on the array.

Solution: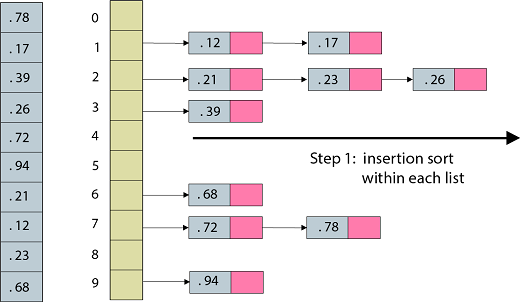

Fig: Bucket sort: step 1, placing keys in bins in sorted order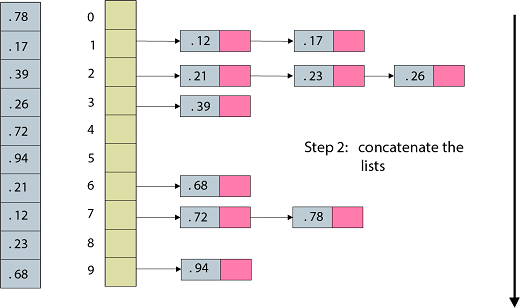

Fig: Bucket sort: step 2, concatenate the lists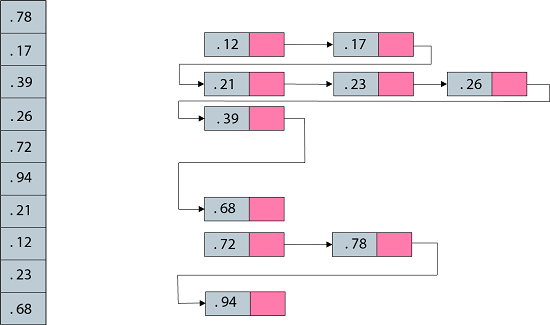

Fig: Bucket sort: the final sorted sequence