Merging NetworkMerging Network is the network that can join two sorted input sequences into one sorted output sequence. We adapt BITONIC-SORTER [n] to create the merging network MERGER [n]. The merging network is based on the following assumption: Given two sorted sequences, if we reverse the order of the second sequence and then connect the two sequences, the resulting sequence is bitonic. For Example: Given two sorted zero-one sequences X = 00000111 and Y =00001111, we reverse Y to get YR = 11110000. Concatenating X and YR yield 0000011111110000, which is bitonic. The sorting network SORTER [n] need the merging network to implement a parallel version of merge sort. The first stage of SORTER [n] consists of n/2 copies of MERGER [2] that work in parallel to merge pairs of a 1-element sequence to produce a sorted sequence of length 2. The second stage subsists of n/4 copies of MERGER [4] that merge pairs of these 2-element sorted sequences to generate sorted sequences of length 4. In general, for k = 1, 2..... log n, stage k consists of n/2k copies of MERGER [2k] that merge pairs of the 2k-1 element sorted sequence to produce a sorted sequence of length2k. At the last stage, one sorted sequence consisting of all the input values is produced. This sorting network can be shown by induction to sort zero-one sequences, and therefore by the zero-one principle, it can sort arbitrary values. The recurrence given the depth of SORTER [n] 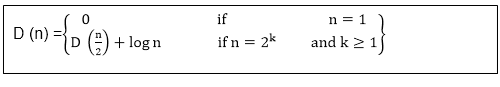
Whose solution is D (n) = θ (log2n). Thus, we can sort n numbers in parallel in ₒ (log2n) time.
Next TopicComplexity Classes
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









