Flow Networks and Flows

Flow Network is a directed graph that is used for modeling material Flow. There are two different vertices; one is a source which produces material at some steady rate, and another one is sink which consumes the content at the same constant speed. The flow of the material at any mark in the system is the rate at which the element moves.

Some real-life problems like the flow of liquids through pipes, the current through wires and delivery of goods can be modeled using flow networks.

Definition: A Flow Network is a directed graph G = (V, E) such that

1. For each edge (u, v) ∈ E, we associate a nonnegative weight capacity c (u, v) ≥ 0.If (u, v) ∉ E, we assume that c (u, v) = 0.
2. There are two distinguishing points, the source s, and the sink t;
3. For every vertex v ∈ V, there is a path from s to t containing v.

Let G = (V, E) be a flow network. Let s be the source of the network, and let t be the sink. A flow in G is a real-valued function f: V x V→R such that the following properties hold:

• Capacity Constraint: For all u, v ∈ V, we need f (u, v) ≤ c (u, v).
• Skew Symmetry: For all u, v ∈ V, we need f (u, v) = - f (u, v).
• Flow Conservation: For all u ∈ V-{s, t}, we need

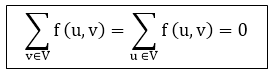
The quantity f (u, v), which can be positive or negative, is known as the net flow from vertex u to vertex v. In the maximum-flow problem, we are given a flow network G with source s and sink t, and we wish to find a flow of maximum value from s to t.

The three properties can be described as follows:

1. Capacity Constraint makes sure that the flow through each edge is not greater than the capacity.
2. Skew Symmetry means that the flow from u to v is the negative of the flow from v to u.
3. The flow-conservation property says that the total net flow out of a vertex other than the source or sink is 0. In other words, the amount of flow into a v is the same as the amount of flow out of v for every vertex v ∈ V - {s, t}

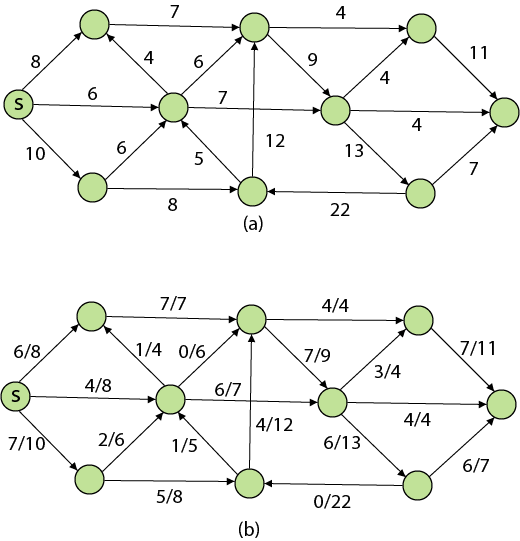
The value of the flow is the net flow from the source,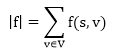

The positive net flow entering a vertex v is described by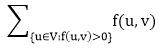

The positive net flow leaving a vertex is described symmetrically. One interpretation of the Flow-Conservation Property is that the positive net flow entering a vertex other than the source or sink must equal the positive net flow leaving the vertex.

A flow f is said to be integer-valued if f (u, v) is an integer for all (u, v) ∈ E. Clearly, the value of the flow is an integer is an integer-valued flow.