Travelling Sales Person Problem

The traveling salesman problems abide by a salesman and a set of cities. The salesman has to visit every one of the cities starting from a certain one (e.g., the hometown) and to return to the same city. The challenge of the problem is that the traveling salesman needs to minimize the total length of the trip.

Suppose the cities are x₁ x₂..... x_n where cost c_ij denotes the cost of travelling from city x_i to x_j. The travelling salesperson problem is to find a route starting and ending at x₁ that will take in all cities with the minimum cost.

Example: A newspaper agent daily drops the newspaper to the area assigned in such a manner that he has to cover all the houses in the respective area with minimum travel cost. Compute the minimum travel cost.

The area assigned to the agent where he has to drop the newspaper is shown in fig: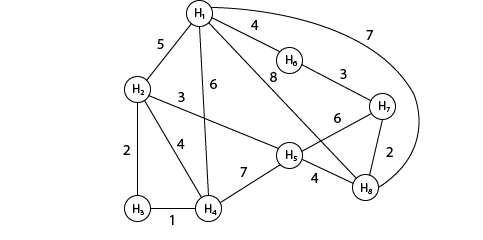

Solution: The cost- adjacency matrix of graph G is as follows:

cost_ij =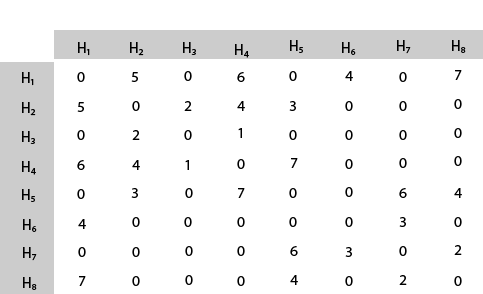

The tour starts from area H₁ and then select the minimum cost area reachable from H₁.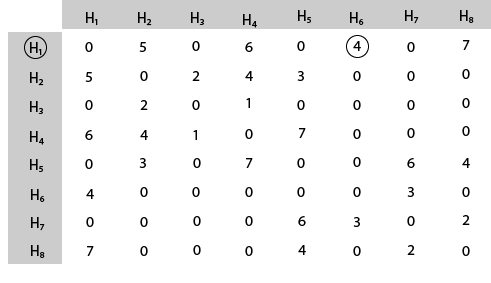

Mark area H₆ because it is the minimum cost area reachable from H₁ and then select minimum cost area reachable from H₆.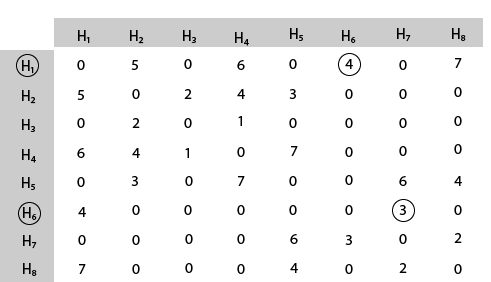

Mark area H₇ because it is the minimum cost area reachable from H₆ and then select minimum cost area reachable from H₇.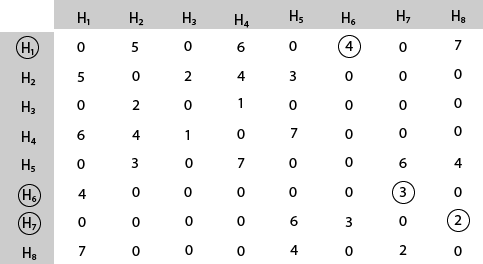

Mark area H₈ because it is the minimum cost area reachable from H₈.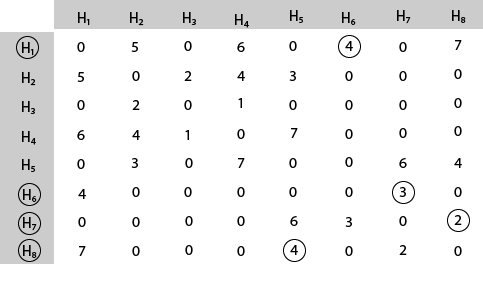

Mark area H₅ because it is the minimum cost area reachable from H₅.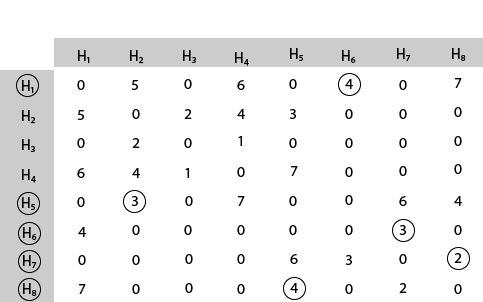

Mark area H₂ because it is the minimum cost area reachable from H₂.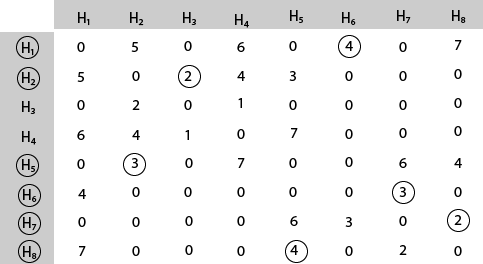

Mark area H₃ because it is the minimum cost area reachable from H₃.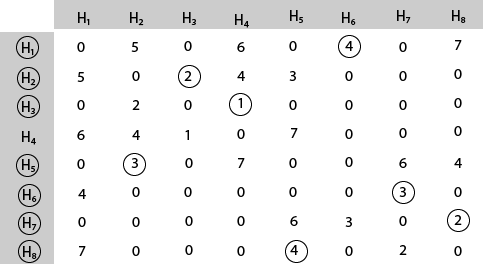

Mark area H₄ and then select the minimum cost area reachable from H₄ it is H₁.So, using the greedy strategy, we get the following.

4    3    2    4    3    2   1    6
H1 → H6 → H7 → H8 → H5 → H2 → H3 → H4 → H1.

Thus the minimum travel cost = 4 + 3 + 2 + 4 + 3 + 2 + 1 + 6 = 25

Matroids:

A matroid is an ordered pair M(S, I) satisfying the following conditions:

1. S is a finite set.
2. I is a nonempty family of subsets of S, called the independent subsets of S, such that if B ∈ I and A ∈ I. We say that I is hereditary if it satisfies this property. Note that the empty set ∅ is necessarily a member of I.
3. If A ∈ I, B ∈ I and |A| <|B|, then there is some element x ∈ B ? A such that A∪{x}∈I. We say that M satisfies the exchange property.

We say that a matroid M (S, I) is weighted if there is an associated weight function w that assigns a strictly positive weight w (x) to each element x ∈ S. The weight function w extends to a subset of S by summation:

w (A) = ∑x∈A w(x)

for any A ∈ S.