Network Flow ProblemsThe most obvious flow network problem is the following: Problem1: Given a flow network G = (V, E), the maximum flow problem is to find a flow with maximum value. Problem 2: The multiple source and sink maximum flow problem is similar to the maximum flow problem, except there is a set {s1,s2,s3.......sn} of sources and a set {t1,t2,t3..........tn} of sinks. Fortunately, this problem is no solid than regular maximum flow. Given multiple sources and sink flow network G, we define a new flow network G' by adding
Figure shows a multiple sources and sinks flow network and an equivalent single source and sink flow network 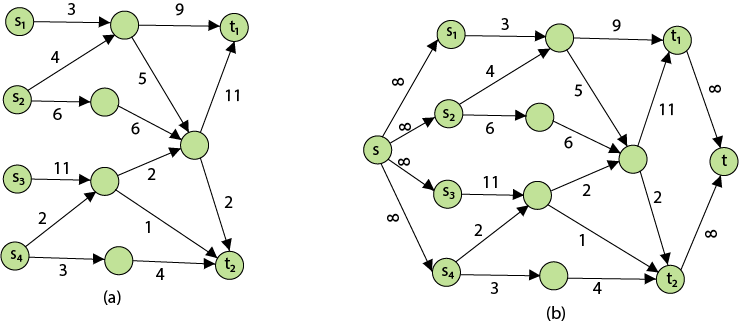
Residual Networks: The Residual Network consists of an edge that can admit more net flow. Suppose we have a flow network G = (V, E) with source s and sink t. Let f be a flow in G, and examine a pair of vertices u, v ∈ V. The sum of additional net flow we can push from u to v before exceeding the capacity c (u, v) is the residual capacity of (u, v) given by 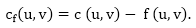
When the net flow f (u, v) is negative, the residual capacity cf (u,v) is greater than the capacity c (u, v). For Example: if c (u, v) = 16 and f (u, v) =16 and f (u, v) = -4, then the residual capacity cf (u,v) is 20. Given a flow network G = (V, E) and a flow f, the residual network of G induced by f is Gf = (V, Ef), where 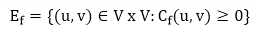
That is, each edge of the residual network, or residual edge, can admit a strictly positive net flow. Augmenting Path: Given a flow network G = (V, E) and a flow f, an augmenting path p is a simple path from s to t in the residual networkGf. By the solution of the residual network, each edge (u, v) on an augmenting path admits some additional positive net flow from u to v without violating the capacity constraint on the edge. Let G = (V, E) be a flow network with flow f. The residual capacity of an augmenting path p is 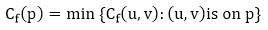
The residual capacity is the maximal amount of flow that can be pushed through the augmenting path. If there is an augmenting path, then each edge on it has a positive capacity. We will use this fact to compute a maximum flow in a flow network. 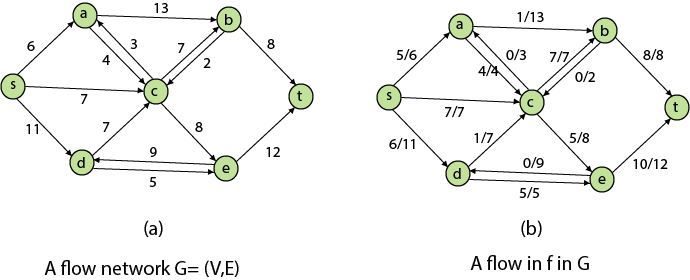 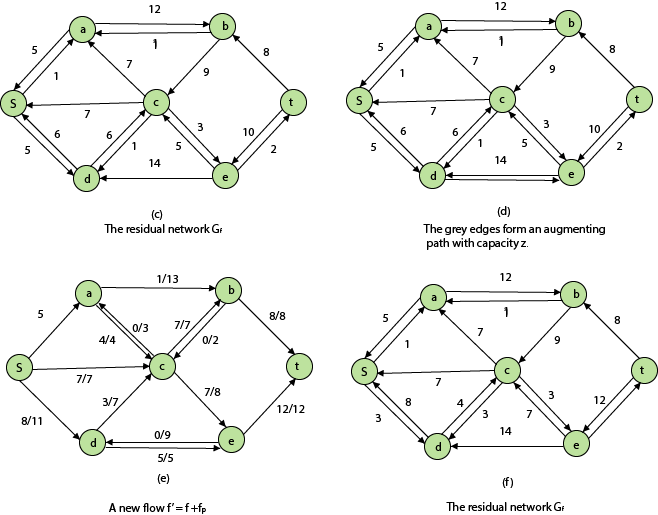
Next TopicFord Fulkerson Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









