Approximate AlgorithmsIntroduction:An Approximate Algorithm is a way of approach NP-COMPLETENESS for the optimization problem. This technique does not guarantee the best solution. The goal of an approximation algorithm is to come as close as possible to the optimum value in a reasonable amount of time which is at the most polynomial time. Such algorithms are called approximation algorithm or heuristic algorithm.
Performance RatiosSuppose we work on an optimization problem where every solution carries a cost. An Approximate Algorithm returns a legal solution, but the cost of that legal solution may not be optimal. For Example, suppose we are considering for a minimum size vertex-cover (VC). An approximate algorithm returns a VC for us, but the size (cost) may not be minimized. Another Example is we are considering for a maximum size Independent set (IS). An approximate Algorithm returns an IS for us, but the size (cost) may not be maximum. Let C be the cost of the solution returned by an approximate algorithm, and C* is the cost of the optimal solution. We say the approximate algorithm has an approximate ratio P (n) for an input size n, where 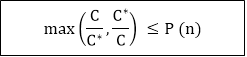
Intuitively, the approximation ratio measures how bad the approximate solution is distinguished with the optimal solution. A large (small) approximation ratio measures the solution is much worse than (more or less the same as) an optimal solution. Observe that P (n) is always ≥ 1, if the ratio does not depend on n, we may write P. Therefore, a 1-approximation algorithm gives an optimal solution. Some problems have polynomial-time approximation algorithm with small constant approximate ratios, while others have best-known polynomial time approximation algorithms whose approximate ratios grow with n.
Next TopicVertex Cover
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










