Longest Common SubsequenceHere longest means that the subsequence should be the biggest one. The common means that some of the characters are common between the two strings. The subsequence means that some of the characters are taken from the string that is written in increasing order to form a subsequence. Let's understand the subsequence through an example. Suppose we have a string 'w'. W1 = abcd The following are the subsequences that can be created from the above string:
The above are the subsequences as all the characters in a sub-string are written in increasing order with respect to their position. If we write ca or da then it would be a wrong subsequence as characters are not appearing in the increasing order. The total number of subsequences that would be possible is 2n, where n is the number of characters in a string. In the above string, the value of 'n' is 4 so the total number of subsequences would be 16. W2= bcd By simply looking at both the strings w1 and w2, we can say that bcd is the longest common subsequence. If the strings are long, then it won't be possible to find the subsequence of both the string and compare them to find the longest common subsequence. Finding LCS using dynamic programming with the help of a table. Consider two strings: X= a b a a b a Y= b a b b a b (a, b) For index i=1, j=1 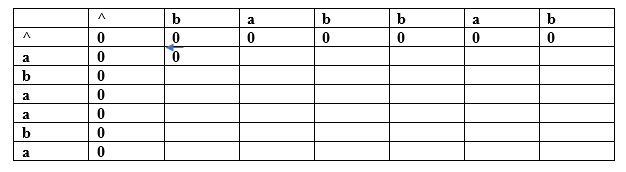
Since both the characters are different so we consider the maximum value. Both contain the same value, i.e., 0 so put 0 in (a,b). Suppose we are taking the 0 value from 'X' string, so we put arrow towards 'a' as shown in the above table. (a, a) For index i=1, j=2 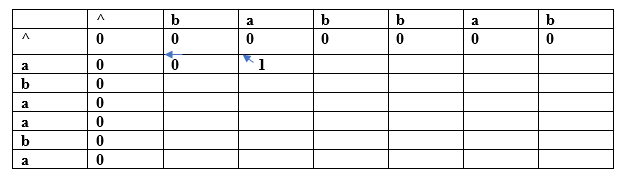
Both the characters are the same, so the value would be calculated by adding 1 and upper diagonal value. Here, upper diagonal value is 0, so the value of this entry would be (1+0) equal to 1. Here, we are considering the upper diagonal value, so the arrow will point diagonally. (a, b) For index i=1, j=3 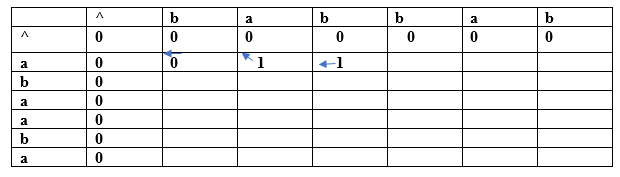
Since both the characters are different so we consider the maximum value. The character 'a' has the maximum value, i.e., 1. The new entry, i.e., (a, b) will contain the value 1 pointing to the 1 value. (a, b) For index i=1, j=4 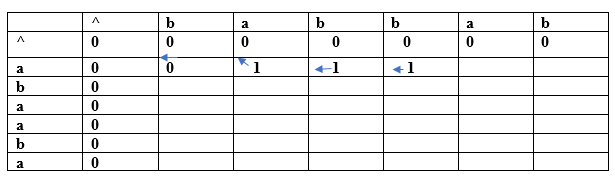
Since both the characters are different so we consider the maximum value. The character 'a' has the maximum value, i.e., 1. The new entry, i.e., (a, b) will contain the value 1 pointing to the 1 value. (a, a) For index i=1, j=5 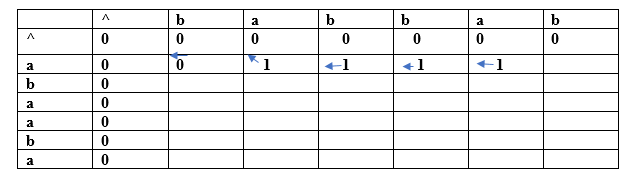
Both the characters are same so the value would be calculated by adding 1 and upper diagonal value. Here, upper diagonal value is 0 so the value of this entry would be (1+0) equal to 1. Here, we are considering the upper diagonal value so arrow will point diagonally. (a, b) For index i=1, j=6 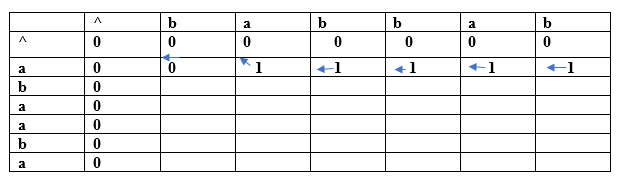
Since both the characters are different so we consider the maximum value. The character 'a' has the maximum value, i.e., 1. The new entry, i.e., (a, b) will contain the value 1 pointing to the 1 value. (b, b) For index i=2, j=1 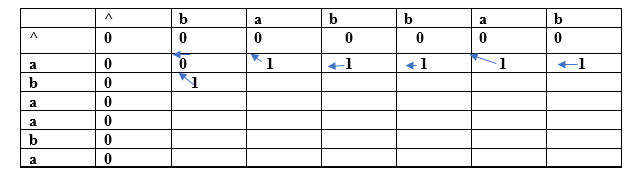
Both the characters are same so the value would be calculated by adding 1 and upper diagonal value. Here, upper diagonal value is 0 so the value of this entry would be (1+0) equal to 1. Here, we are considering the upper diagonal value so arrow will point diagonally. (b, a) For index i=2, j=2 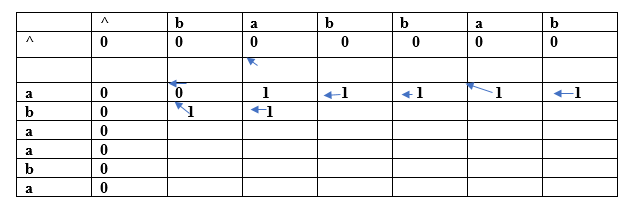
Since both the characters are different so we consider the maximum value. The character 'a' has the maximum value, i.e., 1. The new entry, i.e., (a, b) will contain the value 1 pointing to the 1 value. In this way, we will find the complete table. The final table would be: 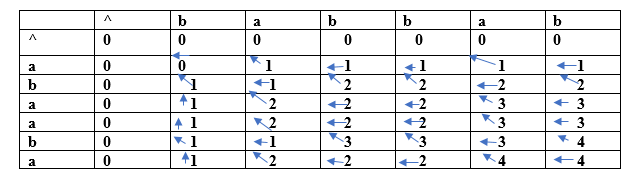
In the above table, we can observe that all the entries are filled. Now we are at the last cell having 4 value. This cell moves at the left which contains 4 value.; therefore, the first character of the LCS is 'a'. The left cell moves upwards diagonally whose value is 3; therefore, the next character is 'b' and it becomes 'ba'. Now the cell has 2 value that moves on the left. The next cell also has 2 value which is moving upwards; therefore, the next character is 'a' and it becomes 'aba'. The next cell is having a value 1 that moves upwards. Now we reach the cell (b, b) having value which is moving diagonally upwards; therefore, the next character is 'b'. The final string of longest common subsequence is 'baba'. Why a dynamic programming approach in solving a LCS problem is more efficient than the recursive algorithm? If we use the dynamic programming approach, then the number of function calls are reduced. The dynamic programming approach stores the result of each function call so that the result of function calls can be used in the future function calls without the need of calling the functions again. In the above dynamic algorithm, the results obtained from the comparison between the elements of x and the elements of y are stored in the table so that the results can be stored for the future computations. The time taken by the dynamic programming approach to complete a table is O(mn) and the time taken by the recursive algorithm is 2max(m, n). Algorithm of Longest Common Subsequence Implementation LCS algorithm in C programming language Output 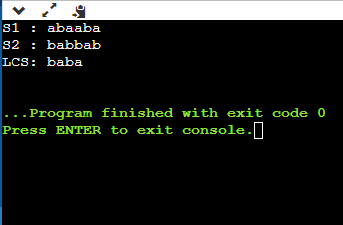
Next TopicTabulation vs Memoization
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









