Red Black TreeA Red Black Tree is a category of the self-balancing binary search tree. It was created in 1972 by Rudolf Bayer who termed them "symmetric binary B-trees." A red-black tree is a Binary tree where a particular node has color as an extra attribute, either red or black. By check the node colors on any simple path from the root to a leaf, red-black trees secure that no such path is higher than twice as long as any other so that the tree is generally balanced. Properties of Red-Black TreesA red-black tree must satisfy these properties:
A tree T is an almost red-black tree (ARB tree) if the root is red, but other conditions above hold. 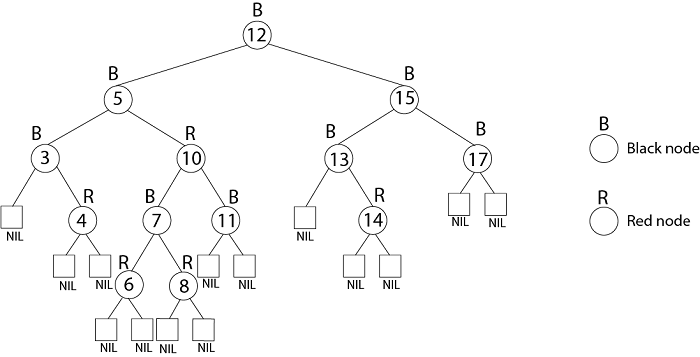
Operations on RB Trees:The search-tree operations TREE-INSERT and TREE-DELETE, when runs on a red-black tree with n keys, take O (log n) time. Because they customize the tree, the conclusion may violate the red-black properties. To restore these properties, we must change the color of some of the nodes in the tree and also change the pointer structure. 1. Rotation:Restructuring operations on red-black trees can generally be expressed more clearly in details of the rotation operation. 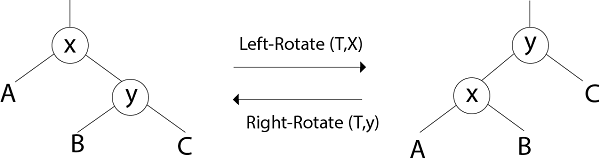
Clearly, the order (Ax By C) is preserved by the rotation operation. Therefore, if we start with a BST and only restructure using rotation, then we will still have a BST i.e. rotation do not break the BST-Property.
LEFT ROTATE (T, x)
1. y ← right [x]
1. y ← right [x]
2. right [x] ← left [y]
3. p [left[y]] ← x
4. p[y] ← p[x]
5. If p[x] = nil [T]
then root [T] ← y
else if x = left [p[x]]
then left [p[x]] ← y
else right [p[x]] ← y
6. left [y] ← x.
7. p [x] ← y.
Example: Draw the complete binary tree of height 3 on the keys {1, 2, 3... 15}. Add the NIL leaves and color the nodes in three different ways such that the black heights of the resulting trees are: 2, 3 and 4. Solution: 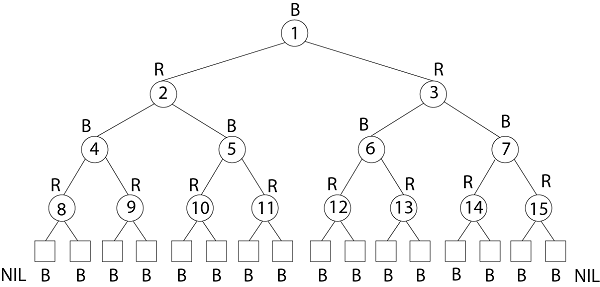
Tree with black-height-2 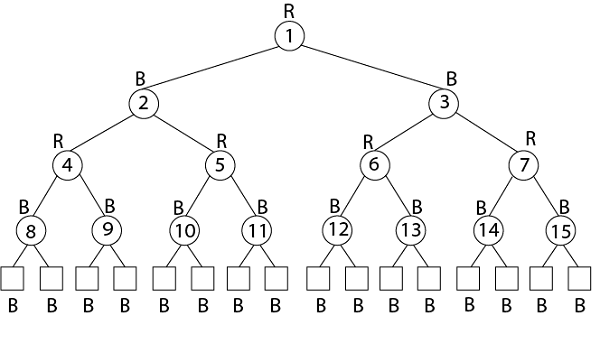
Tree with black-height-3 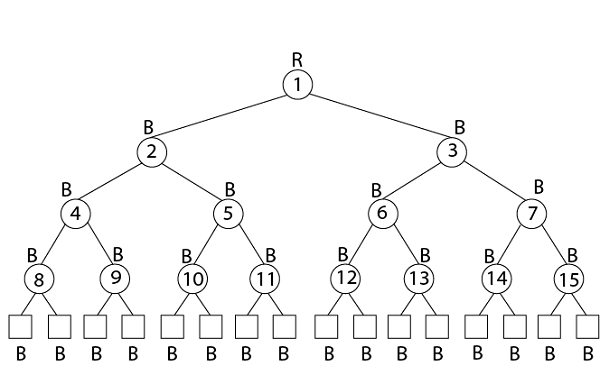
Tree with black-height-4 2. Insertion:
A discrepancy can decision from a parent and a child both having a red color. This type of discrepancy is determined by the location of the node concerning grandparent, and the color of the sibling of the parent. RB-INSERT (T, z) 1. y ← nil [T] 2. x ← root [T] 3. while x ≠ NIL [T] 4. do y ← x 5. if key [z] < key [x] 6. then x ← left [x] 7. else x ← right [x] 8. p [z] ← y 9. if y = nil [T] 10. then root [T] ← z 11. else if key [z] < key [y] 12. then left [y] ← z 13. else right [y] ← z 14. left [z] ← nil [T] 15. right [z] ← nil [T] 16. color [z] ← RED 17. RB-INSERT-FIXUP (T, z) After the insert new node, Coloring this new node into black may violate the black-height conditions and coloring this new node into red may violate coloring conditions i.e. root is black and red node has no red children. We know the black-height violations are hard. So we color the node red. After this, if there is any color violation, then we have to correct them by an RB-INSERT-FIXUP procedure.
RB-INSERT-FIXUP (T, z)
1. while color [p[z]] = RED
2. do if p [z] = left [p[p[z]]]
3. then y ← right [p[p[z]]]
4. If color [y] = RED
5. then color [p[z]] ← BLACK //Case 1
6. color [y] ← BLACK //Case 1
7. color [p[z]] ← RED //Case 1
8. z ← p[p[z]] //Case 1
9. else if z= right [p[z]]
10. then z ← p [z] //Case 2
11. LEFT-ROTATE (T, z) //Case 2
12. color [p[z]] ← BLACK //Case 3
13. color [p [p[z]]] ← RED //Case 3
14. RIGHT-ROTATE (T,p [p[z]]) //Case 3
15. else (same as then clause)
With "right" and "left" exchanged
16. color [root[T]] ← BLACK
Example: Show the red-black trees that result after successively inserting the keys 41,38,31,12,19,8 into an initially empty red-black tree. Solution:Insert 41 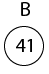 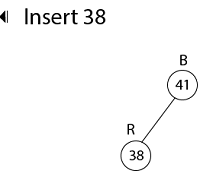 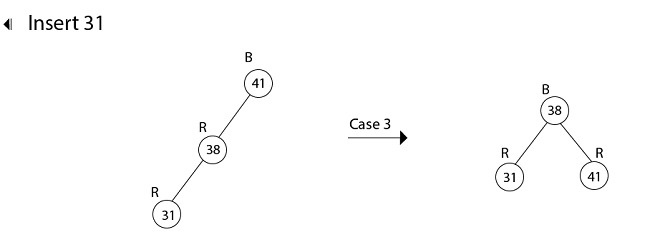 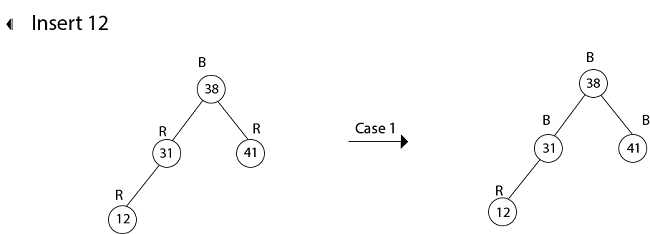 Insert 19 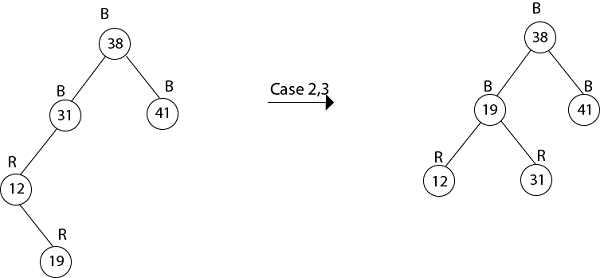 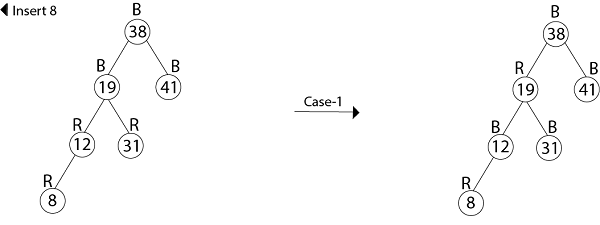
Thus the final tree is 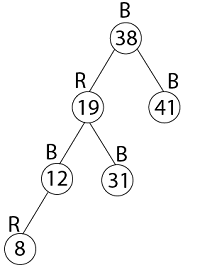
3. Deletion:First, search for an element to be deleted
The strategy RB-DELETE is a minor change of the TREE-DELETE procedure. After splicing out a node, it calls an auxiliary procedure RB-DELETE-FIXUP that changes colors and performs rotation to restore the red-black properties. RB-DELETE (T, z) 1. if left [z] = nil [T] or right [z] = nil [T] 2. then y ← z 3. else y ← TREE-SUCCESSOR (z) 4. if left [y] ≠ nil [T] 5. then x ← left [y] 6. else x ← right [y] 7. p [x] ← p [y] 8. if p[y] = nil [T] 9. then root [T] ← x 10. else if y = left [p[y]] 11. then left [p[y]] ← x 12. else right [p[y]] ← x 13. if y≠ z 14. then key [z] ← key [y] 15. copy y's satellite data into z 16. if color [y] = BLACK 17. then RB-delete-FIXUP (T, x) 18. return y RB-DELETE-FIXUP (T, x) 1. while x ≠ root [T] and color [x] = BLACK 2. do if x = left [p[x]] 3. then w ← right [p[x]] 4. if color [w] = RED 5. then color [w] ← BLACK //Case 1 6. color [p[x]] ← RED //Case 1 7. LEFT-ROTATE (T, p [x]) //Case 1 8. w ← right [p[x]] //Case 1 9. If color [left [w]] = BLACK and color [right[w]] = BLACK 10. then color [w] ← RED //Case 2 11. x ← p[x] //Case 2 12. else if color [right [w]] = BLACK 13. then color [left[w]] ← BLACK //Case 3 14. color [w] ← RED //Case 3 15. RIGHT-ROTATE (T, w) //Case 3 16. w ← right [p[x]] //Case 3 17. color [w] ← color [p[x]] //Case 4 18. color p[x] ← BLACK //Case 4 19. color [right [w]] ← BLACK //Case 4 20. LEFT-ROTATE (T, p [x]) //Case 4 21. x ← root [T] //Case 4 22. else (same as then clause with "right" and "left" exchanged) 23. color [x] ← BLACK Example: In a previous example, we found that the red-black tree that results from successively inserting the keys 41,38,31,12,19,8 into an initially empty tree. Now show the red-black trees that result from the successful deletion of the keys in the order 8, 12, 19,31,38,41. Solution: 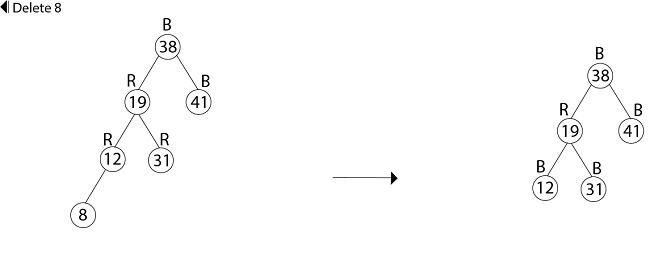 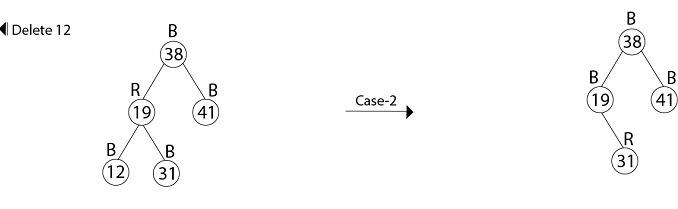 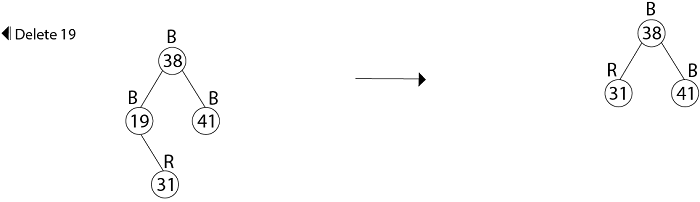 
Delete 38 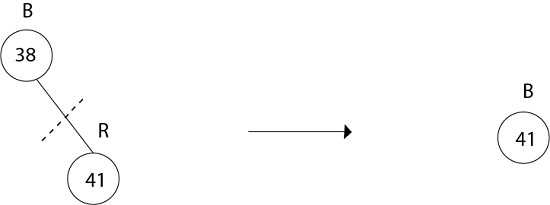
Delete 41 No Tree.
Next TopicDynamic Programming
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










