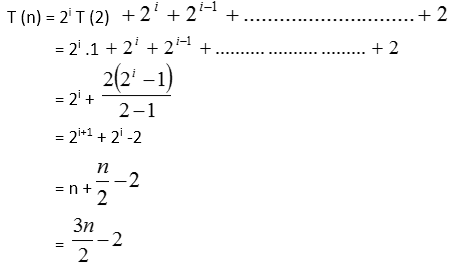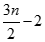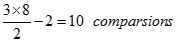Max - Min ProblemProblem: Analyze the algorithm to find the maximum and minimum element from an array. Algorithm: Max ?Min Element (a []) Max: a [i] Min: a [i] For i= 2 to n do If a[i]> max then max = a[i] if a[i] < min then min: a[i] return (max, min) Analysis:Method 1: if we apply the general approach to the array of size n, the number of comparisons required are 2n-2. Method-2: In another approach, we will divide the problem into sub-problems and find the max and min of each group, now max. Of each group will compare with the only max of another group and min with min. Let n = is the size of items in an array
Let T (n) = time required to apply the algorithm on an array of size n. Here we divide the terms as T(n/2). 2 here tends to the comparison of the minimum with minimum and maximum with maximum as in above example.
T (n) = 2 T T (2) = 1, time required to compare two elements/items. (Time is measured in units of the number of comparisons)
Put eq (ii) in eq (i)
Similarly, apply the same procedure recursively on each subproblem or anatomy {Use recursion means, we will use some stopping condition to stop the algorithm}
Recursion will stop, when Put the equ.4 into equation3.
Number of comparisons requires applying the divide and conquering algorithm on n elements/items = Number of comparisons requires applying general approach on n elements = (n-1) + (n-1) = 2n-2 From this example, we can analyze, that how to reduce the number of comparisons by using this technique. Analysis: suppose we have the array of size 8 elements. Method1: requires (2n-2), (2x8)-2=14 comparisons It is evident; we can reduce the number of comparisons (complexity) by using a proper technique.
Next TopicBinary Search
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





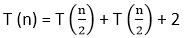
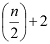 → Eq (i)
→ Eq (i)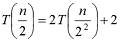 → Eq (ii)
→ Eq (ii)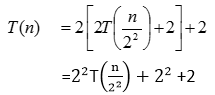
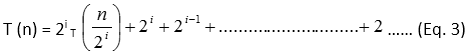
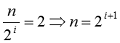 → (Eq. 4)
→ (Eq. 4)