Maximum Bipartite MatchingA Bipartite Graph is a graph whose vertices can be divided into two independent sets L and R such that every edge (u, v) either connect a vertex from L to R or a vertex from R to L. In other words, for every edge (u, v) either u ∈ L and v ∈ L. We can also say that no edge exists that connect vertices of the same set. 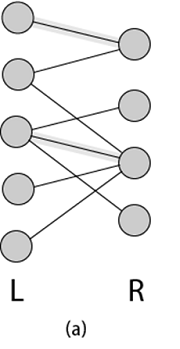 Matching is a Bipartite Graph is a set of edges chosen in such a way that no two edges share an endpoint. Given an undirected Graph G = (V, E), a Matching is a subset of edge M ⊆ E such that for all vertices v ∈ V, at most one edge of M is incident on v. A Maximum matching is a matching of maximum cardinality, that is, a matching M such that for any matching M', we have|M|>|M' |. Finding a maximum bipartite matchingWe can use the Ford-Fulkerson method to find a maximum matching in an undirected bipartite graph G= (V, E) in time polynomial in |V| and |E|. The trick is to construct a flow network G= (V',E') for the bipartite graph G as follows. We let the source s and sink t be new vertices not in V, and we let V'=V ∪{s,t}.If the vertex partition of G is V = L∪R, the directed edges of G' are the edges of E, directed from L to R, along with |V| new directed edges: 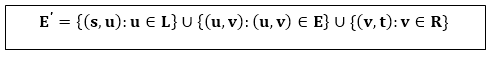
Fig: A Bipartite Graph G = (V, E) with vertex partition V = L ∪ R. 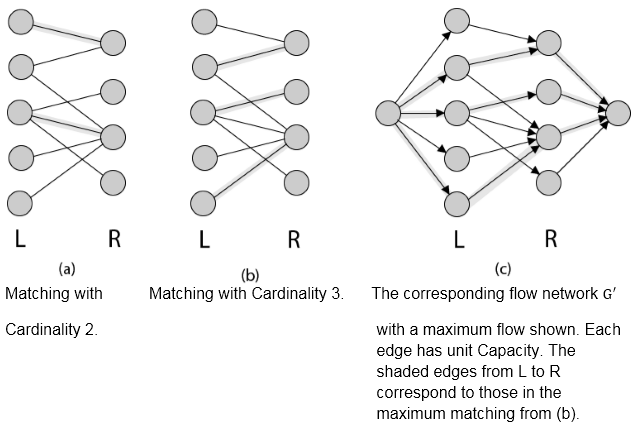
Next TopicComparison Network
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










