Tower of Hanoi1. It is a classic problem where you try to move all the disks from one peg to another peg using only three pegs. 2. Initially, all of the disks are stacked on top of each other with larger disks under the smaller disks. 3. You may move the disks to any of three pegs as you attempt to relocate all of the disks, but you cannot place the larger disks over smaller disks and only one disk can be transferred at a time. This problem can be easily solved by Divide & Conquer algorithm 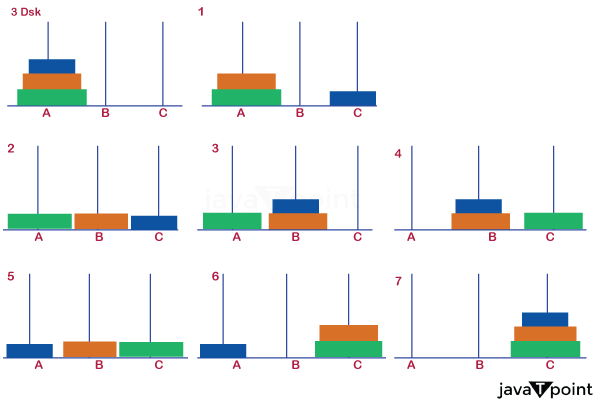
In the above 7 step all the disks from peg A will be transferred to C given Condition:
Let T (n) be the total time taken to move n disks from peg A to peg C
So, total time taken T (n) = T (n-1)+1+ T(n-1) Relation formula for Tower of Hanoi is: 
We get, 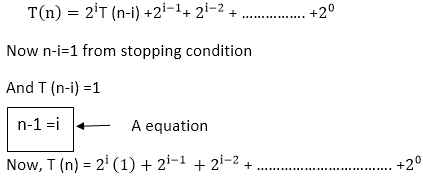
It is a Geometric Progression Series with common ratio, r=2 
B equation is the required complexity of technique tower of Hanoi when we have to move n disks from one peg to another. T (3) = 23- 1 [As in concept we have proved that there will be 7 steps now proved by general equation] Program of Tower of Hanoi:Output: Enter the number of disks: 3 The sequence of moves involved in the Tower of Hanoi is Move disk 1 from peg A to peg C Move disk 2 from peg A to peg B Move disk 1 from peg C to peg B Move disk 3 from peg A to peg C Move disk 1 from peg B to peg A Move disk 2 from peg B to peg C Move disk 1 from peg A to peg 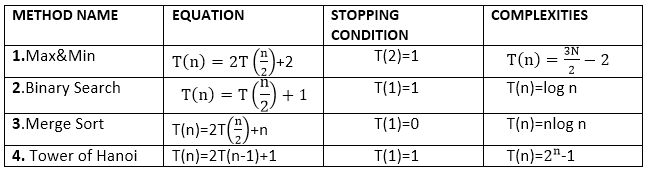
Next TopicBinary Heap Sort
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










