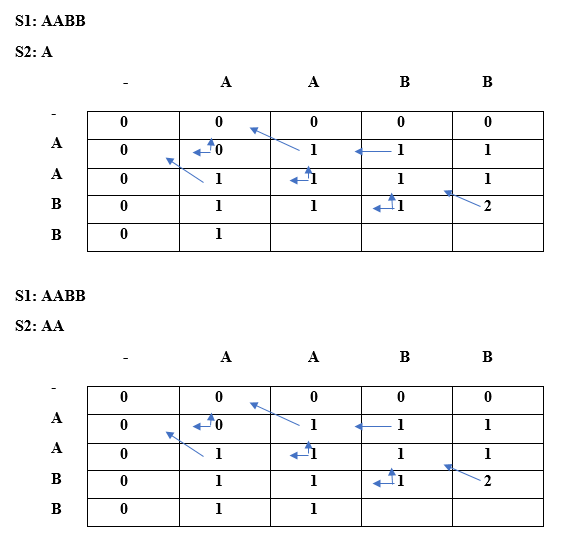
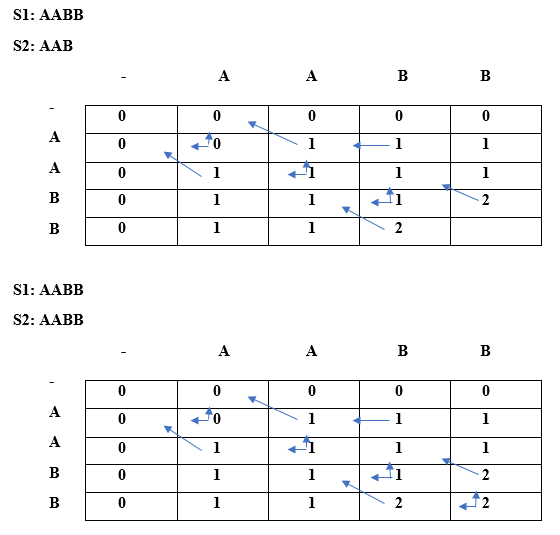
Longest Repeated Subsequence

The longest repeated subsequence states that in a given string; the length of the longest repeated subsequence should be such that the two subsequences should not have the character at the same position, i.e., i^th character in the given two subsequences should not have the same index in the original string. The subsequence means that when we remove one or more elements from the given string and make a new string.

Aim: It is used to find the Longest Repeating Subsequence. It finds the LRS length, and LRS string.

Constraint: The i^th character of two subsequences should not have same index in string S.

Example 1:

Input String: AAB

Subsequence s1: A

Subsequence s2: A

The above are the two subsequences whose length is 1. The 'B' character cannot be considered in the above two subsequence as it would be at the same index of the original string.

Example 2:

Input String: AABB

Subsequence s1: AB

Subsequence s2: AB

The above are the two subsequences whose length is 2. In both the subsequences, 'A' has the different indices in the original string, i.e., first and second index respectively and 'B' has the different indices in the original string, i.e., third and fourth index respectively.

Example 3:

Input String: AABEBCDD

Subsequence s1: ABD

Subsequence s2: ABD

The above are the two subsequences whose length is 3. In both the subsequences, 'A' has the different indices in the original string, i.e., 1^st and 2^nd index respectively, 'B' has the different indices in the original string, i.e., 3^rd and 5^th index respectively, and 'D' has the different indices in the original string, i.e., 7^th and 8^th index respectively.

Example 4:

Input string is: AABEBECDD

The longest repeating subsequence is "ABED"

The length of the longest repeating subsequence is 4.

Example 5:

Input string is: "abcd"

Since there is no character exists that occurs more than once so no repeating subsequence would be exist in the above given string.

Example 6:

Input string is: "bbc"

The longest repeated subsequence is 'b' as 'b' is repeated twice and we cannot consider 'c' character as it would be at the same index in both the subsequences.

Example 7:

Input string is "a b x a y b c d c"

The longest repeated subsequence is "abc" because in both the subsequences; the characters 'a', 'b' and 'c' occur at the different index in both the subsequences.

The length of the longest repeated subsequence is 3.

Important Example

Input string: A X X X

0 1 2 3

S: A X X X

Subsequence s1: X X

1 2

Subsequence s2: X X

2 3

As we can observe in the above two subsequences that the corresponding characters have the different index in the original string. Therefore, they are valid.

Similarity with LCS

Consider the string which is given below:

S: AABBX

Index of each character in a string is given below:

0 1 2 3 4

S: A A B B X

The LCS of the given string would be:

S: AABBX

The LRS of the given string would be:

S1: AB

S2: AB

The above are the two subsequences whose length is 2. In both the subsequences, 'A' has the different indices in the original string, i.e., the index of 'A' in S1 is 0 and the index of 'A' in S2 is 1. The indices of character 'B' in both the subsequences are also different, i.e., the index of 'B' in S1 is 2 and the index of 'B' in S2 is 3.

LRS = LCS (excluding chars at the same index)

Note: There must be multiple instances of chars available to contribute to LRS.

Find LCS excluding chars at same index?

0 1 2

S1: X X X

S2: X X X

The above two subsequences are the same, i.e., XXX. If we consider X at index 0 in S1 and X at index 1 in S2, and consider X at index 1 in S1 and X at index 2 in S2. So, XX would be Longest common subsequence which is of largest length and this is also would be the longest repeated subsequence. The length of LCS and LRS is 2.

Algorithm

Let's dry run to find the LCS excluding chars at the same index.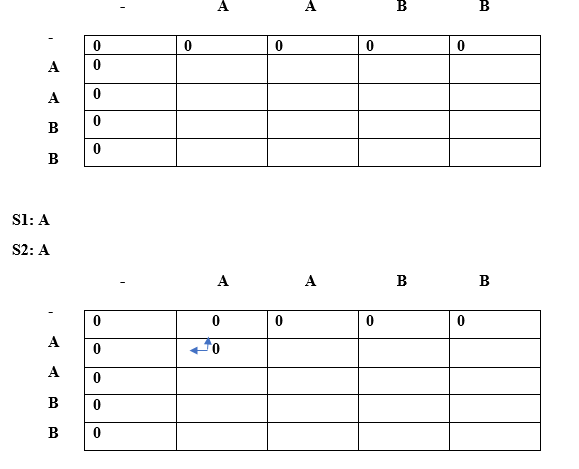

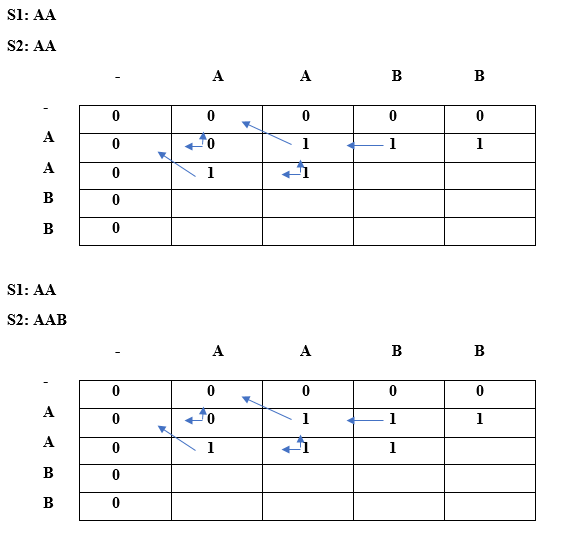
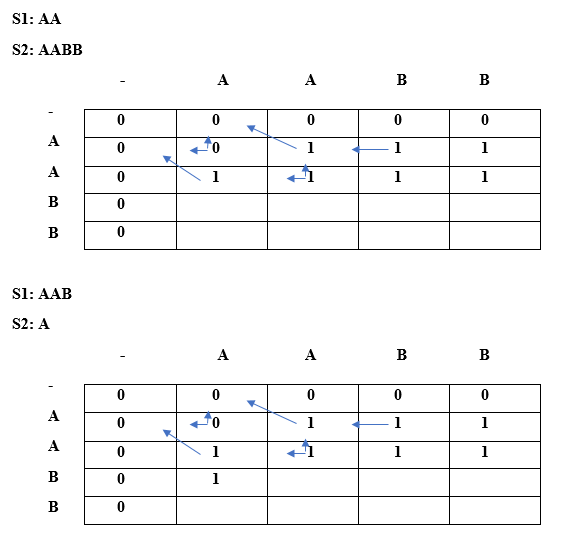
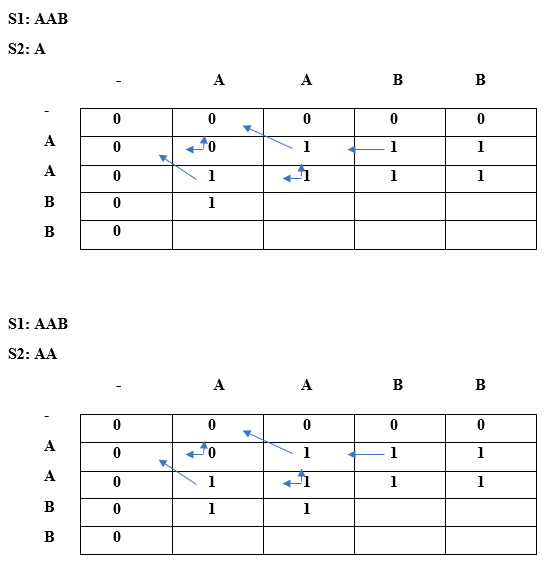
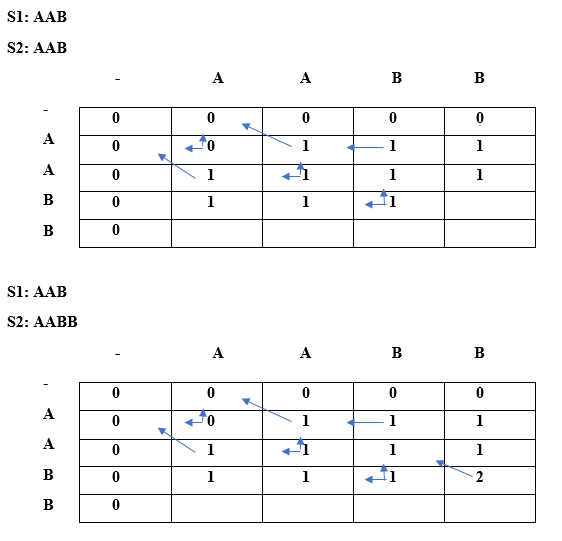
We can observe in the above table that the length of the longest repeated subsequence is 2.

Now we will find out the LRS String. The same algorithm will also be used here. Instead of taking LCS array of integer type, we will take LCS array of string type.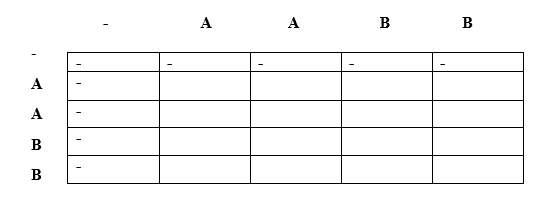

First, we will put '-' under the empty string as shown in the above table.

When i =0, j=0

Since lcs[i] = lcs[j], i.e., 'A', and i==j, so case 3 condition is satisfied according to the algorithm. Therefore, '-' would appear at lcs[0][0] as shown in the below table: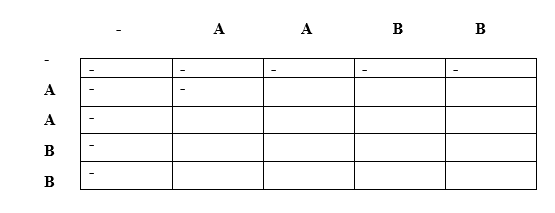

When i=0, j=1

Since lcs[i]=lcs[j] but i!=j so case 2 condition is satisfied. Here, lcs[0][1] = A + " " = A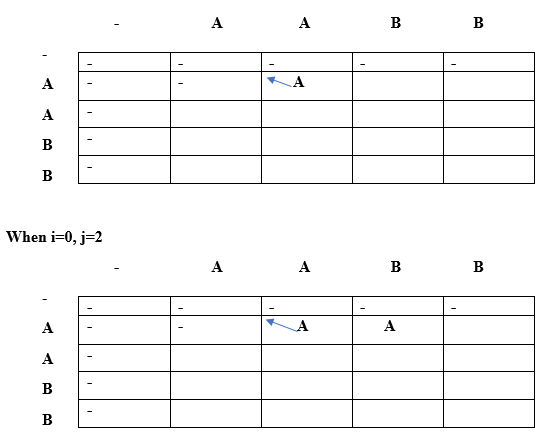

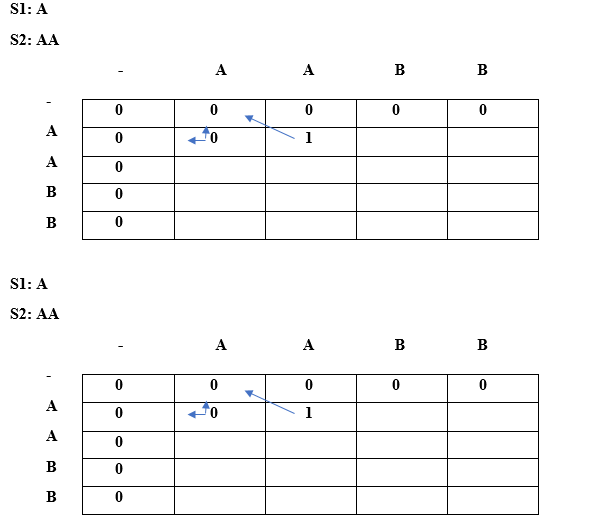
Since lcs[0]!= lcs[2] so we will take the maximum of top and left.

Lcs[0][2] = max(lcs[i-1][j], lcs[i][j-1])

Max(" ", 'A') // The maximum value is 'A' so lcs[0][2] is equal to 'A'.

When i=0, j=3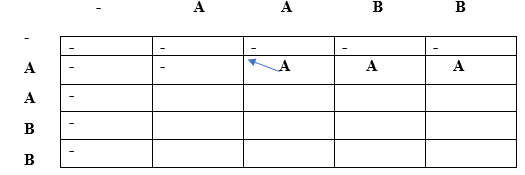

Since lcs[0]!= lcs[3] so we will take the maximum of top and left.

Lcs[0][2] = max(lcs[i-1][j], lcs[i][j-1])

Max(" ", 'A') // The maximum value is 'A' so lcs[0][3] is equal to 'A'.

When i=1, j=0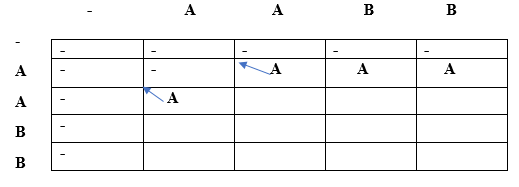

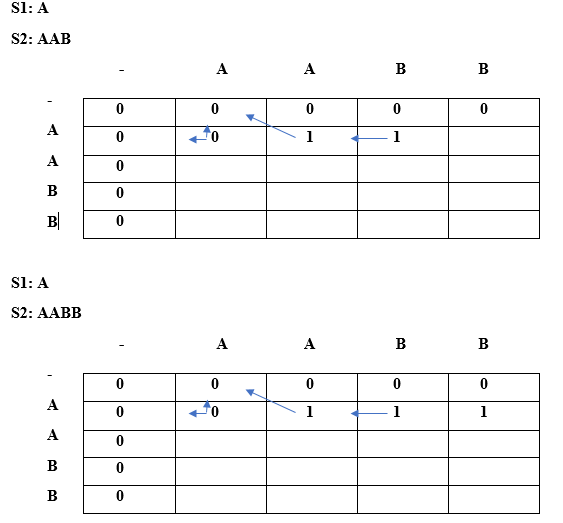
Since lcs[i] is equal to lcs[j], i.e., 'A' but i!=j so lcs[1][0] equals to (diagonal element + current element). Therefore, lcs[1][0] is equal to (" " + 'A') = 'A'.

When i=1, j=1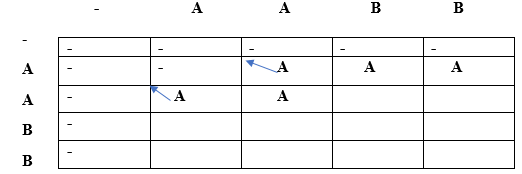

Since lcs[i] = lcs[j], i.e., A and i==j so condition 3 is satisfied according to the algorithm. The lcs[1][1] would be the maximum of top and left. Both top and left are same, i.e., A so lcs[1][1] will be equal to 'A'.

When i=1, j=2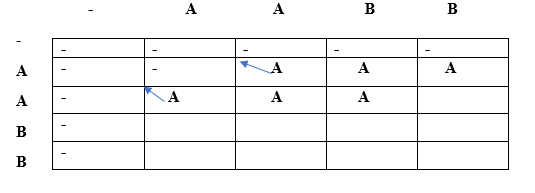

Since lcs[i] is not equal to lcs[j] and i is not equal to j so lcs[i][j] would be the maximum of top and left. Both top and left are same, i.e., A so lcs[1][2] will be equal to 'A'.

When i=1, j=3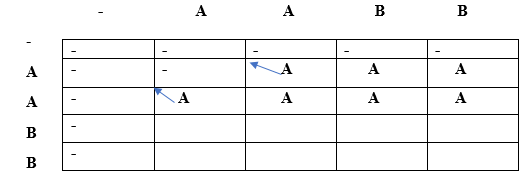

Since lcs[i] is not equal to lcs[j] and i is not equal to j so lcs[i][j] would be the maximum of top and left. Both top and left are same, i.e., A so lcs[1][2] will be equal to 'A'.

When i=2, j=0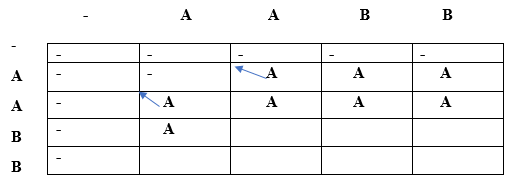

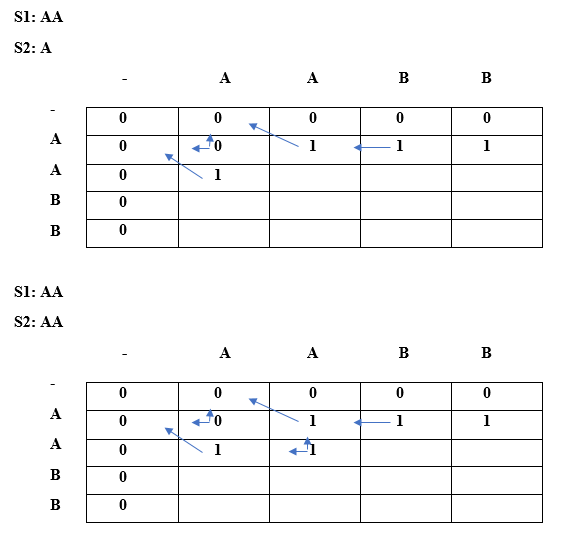
Since lcs[i] is not equal to lcs[j] and i is not equal to j so lcs[i][j] would be the maximum of top and left. Both top and left are same, i.e., A so lcs[2][0] will be equal to 'A'.

When i=2, j=1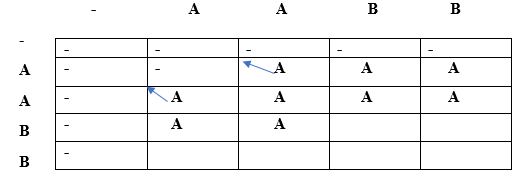

Since lcs[i] is not equal to lcs[j] and their indices are also different so condition 3 is satisfied. Therefore, the lcs[2][1] would be the maximum of top and left. Both the top and left are same, i.e., A, so lcs[2][1] would be equal to 'A'.

When i=2, j=2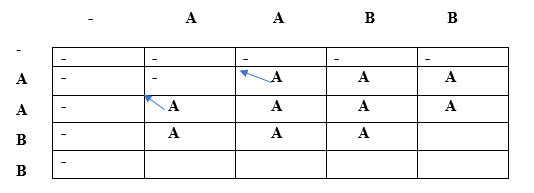

Since lcs[i] is equal to lcs[j] and 'i' is also equal to 'j' so condition 3 is satisfied. Therefore, lcs[i][j] would be the maximum of top and left. Both the top and left are same, i.e., A so lcs[2][2] would be equal to 'A'.

When i=2, j=3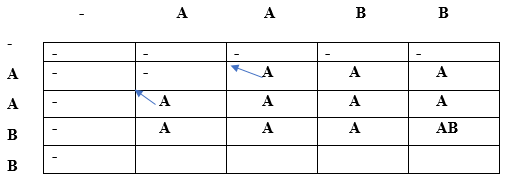

Since lcs[i] is equal to lcs[j] and 'i' is not equal to 'j' so condition 2 is satisfied. Therefore, the lcs[2][3] would be equal to (diagonal element + current element) = A + B = AB.

Similarly, we will fill the last row and obtain the table which is shown below: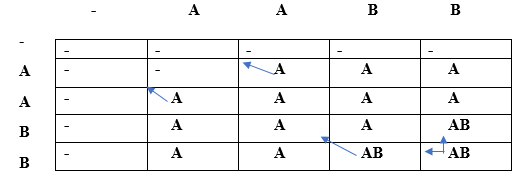

As we can observe in the above table that AB is the longest repeating subsequence. We have basically found the LCS by using the constraint that (i==j) and s[i] == s[j] then it will not contribute to the repeating subsequence otherwise it will contribute.