Hamiltonian Circuit Problems

Given a graph G = (V, E) we have to find the Hamiltonian Circuit using Backtracking approach. We start our search from any arbitrary vertex say 'a.' This vertex 'a' becomes the root of our implicit tree. The first element of our partial solution is the first intermediate vertex of the Hamiltonian Cycle that is to be constructed. The next adjacent vertex is selected by alphabetical order. If at any stage any arbitrary vertex makes a cycle with any vertex other than vertex 'a' then we say that dead end is reached. In this case, we backtrack one step, and again the search begins by selecting another vertex and backtrack the element from the partial; solution must be removed. The search using backtracking is successful if a Hamiltonian Cycle is obtained.

Example: Consider a graph G = (V, E) shown in fig. we have to find a Hamiltonian circuit using Backtracking method.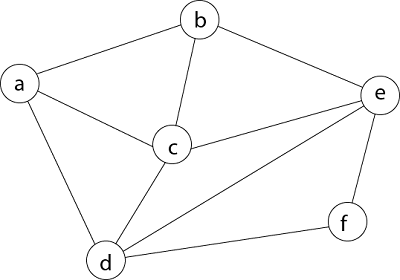

Solution: Firstly, we start our search with vertex 'a.' this vertex 'a' becomes the root of our implicit tree.

Next, we choose vertex 'b' adjacent to 'a' as it comes first in lexicographical order (b, c, d).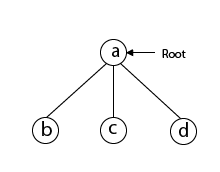

Next, we select 'c' adjacent to 'b.'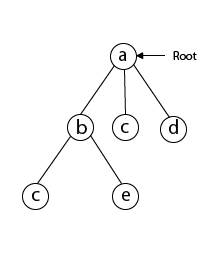

Next, we select 'd' adjacent to 'c.'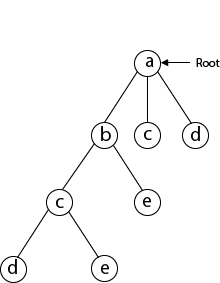

Next, we select 'e' adjacent to 'd.'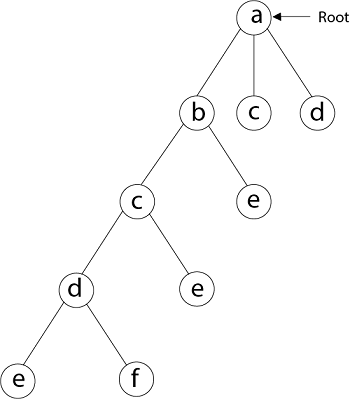

Next, we select vertex 'f' adjacent to 'e.' The vertex adjacent to 'f' is d and e, but they have already visited. Thus, we get the dead end, and we backtrack one step and remove the vertex 'f' from partial solution.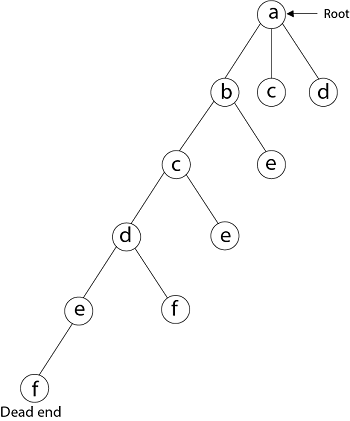

From backtracking, the vertex adjacent to 'e' is b, c, d, and f from which vertex 'f' has already been checked, and b, c, d have already visited. So, again we backtrack one step. Now, the vertex adjacent to d are e, f from which e has already been checked, and adjacent of 'f' are d and e. If 'e' vertex, revisited them we get a dead state. So again we backtrack one step.

Now, adjacent to c is 'e' and adjacent to 'e' is 'f' and adjacent to 'f' is 'd' and adjacent to 'd' is 'a.' Here, we get the Hamiltonian Cycle as all the vertex other than the start vertex 'a' is visited only once. (a - b - c - e - f -d - a).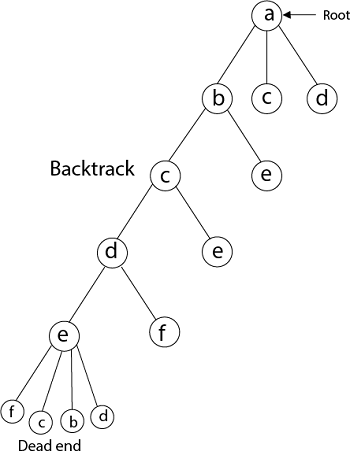

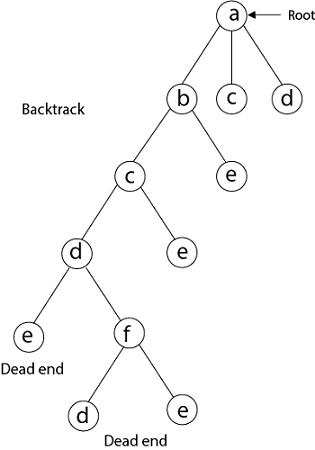
Again Backtrack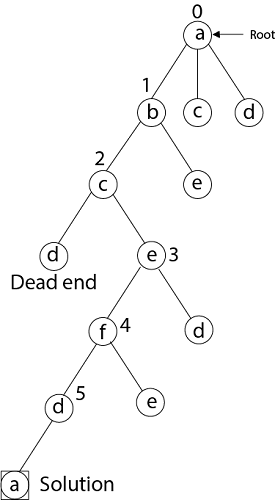

Here we have generated one Hamiltonian circuit, but another Hamiltonian circuit can also be obtained by considering another vertex.