PageRank Algorithm

Introduction

PageRank is an algorithm developed by Google founders Larry Page and Sergey Brin that measures the relevance or importance of web pages on the Internet. Introduced in the late 1990s, it revolutionized web search by providing a method for ranking web pages based on their overall influence and popularity. The PageRank algorithm treats the web as a vast network of interconnected pages. Each page is represented on the web as a node with links between pages at the edges. The basic principle of PageRank is that a page is considered more important if other vital pages link it. The algorithm determines the initial PageRank value for each web page. This initial value can be uniform or based on certain factors, such as the number of incoming links to the page. The algorithm then repeatedly calculates the PageRank value of each page, taking into account the PageRank value of the pages that are related to the pages. During each iteration, the PageRank value of the page is updated based on the sum of the PageRank values of the incoming links. Pages with more inbound links have a more significant impact on the landing page's PageRank.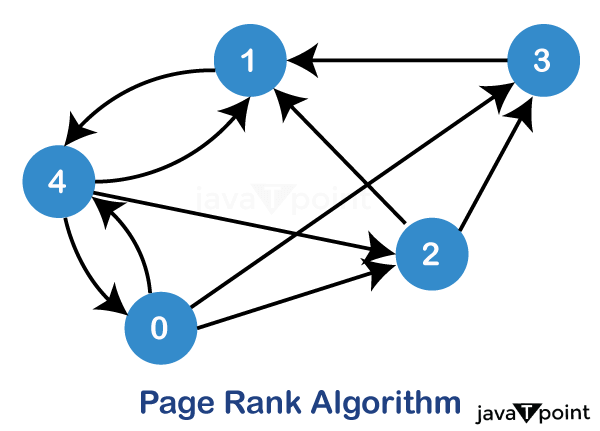

Additionally, a page's PageRank is divided by its number of outbound links, which divides its influence on the pages it links to. The iterative process continues until the PageRank values converge, indicating that the algorithm has reached a stable rank. The resulting PageRank scores describe the relative importance of each web page. Pages with a higher PageRank score are considered more influential and likely to appear higher in search engines. PageRank was a breakthrough in Internet search because it provided a quantitative measure of the importance of a page that was largely independent of keyword searches and other traditional ranking factors. Although search engines use more sophisticated algorithms today, PageRank remains an essential concept in information retrieval and lays the foundation for many further developments in Internet ranking and link analysis.

The History of the PageRank Algorithm

The PageRank algorithm dates back to the late 1990s when Larry Page and Sergey Brin, Ph.D. Stanford University students developed this concept in their search engine research project. The algorithm was named after Larry Page, although "PageRank" was coined later. Page and Brin noted that earlier search engines relied primarily on keyword searches, often producing unsatisfactory results. They believed that the meaning and relevance of a web page should be determined by more than just specific keywords.

Inspired by academic citation analysis, where the importance of a research article is determined by the number and quality of citations, Page, and Brin developed a similar concept for the web. They considered web page nodes in the graph and links between pages as votes of confidence or endorsements.

The idea was that a page that gets more backlinks from other important pages should be considered more influential. In 1996, Page and Brin published the paper "Anatomy of a Large-Scale Hypertext Web Search Engine," describing their approach to web search and introducing the concept of PageRank. They proposed a mathematical algorithm that could calculate the importance of web pages based on the link structure of a network.

The original version of the PageRank algorithm was relatively simple. It treated all pages equally and assigned them a single initial PageRank value. The algorithm then iteratively updated the PageRank of each page based on the votes received from incoming links. Pages with more inbound links had more weight and had a more significant influence on the PageRank of other pages. The publication of the first version of the Google search engine in 1998 marked the practical implementation of the PageRank algorithm. Google quickly gained popularity due to the quality of its search results, which were often more relevant than those of competing search engines. Over time, PageRank evolved and became more complex.

Google has introduced improvements to address potential issues such as link spamming and manipulation. They introduced factors such as mitigation, which reduced the impact of substantial link structures, and personalized PageRank, which personalized search results based on user preferences. PageRank and other factors became essential to Google's ranking algorithm, allowing the search engine to provide more accurate and relevant search results. Although Google's ranking algorithms have become increasingly sophisticated, PageRank remains a fundamental concept in information retrieval, influencing modern search engine technology.

Pseudocode of Page-Rank Algorithm

Input: 
- Graph G with n nodes (web pages)
- Damping factor d (typically set to 0.85)
- Maximum number of iterations max_iterations
- Tolerance threshold tol

Initialize:
- Set the initial PageRank value for all nodes to 1/n

Iterative Algorithm:
for iteration in range(max_iterations):
    new_rank = {}
    for node in G.nodes:
        new_rank[node] = (1 - d) / n  # Initialize with (1 - d)/n, where n is the total number of nodes

    for node in G.nodes:
        for neighbor in G.neighbors(node):
            num_neighbors = len(G.neighbors(neighbor))
            new_rank[neighbor] += d * (current_rank[node] / num_neighbors)  # Update the rank of the neighbor

    # Check for convergence
    max_diff = max(abs(new_rank[node] - current_rank[node]) for node in G.nodes)
    if max_diff < tol:
        break

    current_rank = new_rank  # Update the current rank with the newly calculated ranks

How does Page-Rank algorithm Works?

The PageRank algorithm assigns a numerical value called a PageRank score to each web page in a linked page network. Points indicate the relevance or importance of the page online. The algorithm works step by step:

Initialization: The algorithm begins by determiningthe initial PageRank value of each web page. Typically, this initial value is set uniformly across all pages so that every page has the same initial value.
Link analysis:The algorithm analyzes the links between web pages. It considers both inbound links (links pointing to a page) and outbound links (links from a page to other pages). Pages with more inbound links are considered more important because they are believed to receive recommendations or votes of trust from other important pages.
Iterative calculation:The algorithm repeatedly updates the PageRank score of each page based on the PageRank score of the related pages. During each iteration, the PageRank of a page is recalculated, taking into account the PageRank contribution of its incoming links. Damping factor: a damping factor (typically 0.85) is introduced to avoid infinite loops and ensure the algorithm This indicates that the user will likely continue browsing by following a link on the current page rather than jumping to a random page. The damping factor helps to evenly distribute the importance and block the entire PageRank value on a single page.
Rank Distribution:As the algorithm progresses, the PageRank of the page is distributed among the outgoing links. For example, if a page has a high PageRank and many outbound links, each link will contribute to the overall impact of the page. This division ensures that the importance of linked pages is shared.
Convergence:The iterative process continues until the PageRank score stabilizes or converges. Convergence occurs when the difference in PageRank scores between successive iterations falls below a certain threshold. At this point, the algorithm has reached a stable ranking, and the PageRank scores indicate the relative importance of each web page.
Ranking and Display:Pages are ranked based on their final PageRank scores. Pages with a higher PageRank score are considered more influential or essential Search engines can use these points to display search results, so pages with higher rankings are usually shown closer to the top. By considering the link structure and updating the PageRank score iteratively, the algorithm effectively measures the importance of web pages relative to others. It allows ranking pages based on their popularity and influence, helping to develop more accurate and relevant search engines.

Advantages of Page-Rank Algorithm

The PageRank algorithm, developed by Larry Page and Sergey Brin at Google, is a critical component of Google's search engine algorithm. It revolutionized how web pages are ranked and provided several advantages over traditional ranking methods. Here are some advantages of the PageRank algorithm:

Objective and unbiased: PageRank algorithm is based on the web's link structure rather than solely on content analysis. It measures the importance of a web page based on the number and quality of incoming links from other pages. This approach reduces the impact of subjective factors and manipulation, making the ranking more objective and unbiased.
Quality-focused: PageRank assigns higher importance to pages linked by other essential and trustworthy pages. It considers the authority and reputation of the linking pages, effectively measuring the quality of content. This approach helps filter out spam or low-quality pages, ensuring that highly relevant and reliable pages are ranked higher.
Resilience to manipulation: PageRank is designed to resist manipulation and spamming techniques. The algorithm considers the entire web graph and the collective influence of all pages. It is difficult for web admins to artificially inflate their page rankings by creating numerous low-quality links or manipulating the anchor text. This makes the algorithm more reliable and trustworthy.
Scalability: The PageRank algorithm is highly scalable and can handle large-scale web graphs efficiently. It doesn't require re-indexing or analyzing the entire web each time a search query is performed. Instead, it calculates and stores the PageRank values for web pages, allowing for quick retrieval and ranking during search queries.
Query-independent: PageRank is a query-independent ranking algorithm that doesn't depend on specific search terms. The ranking is determined based on the overall link structure and importance of pages rather than the relevance to a particular query. This allows for consistent and stable rankings across different search queries, ensuring a more robust search experience.
Foundation for other algorithms: The PageRank algorithm forms the foundation for various ranking algorithms and search engine techniques. It has inspired the development of advanced algorithms such as HITS (Hyperlink-Induced Topic Search) and Trust Rank, further improving search results' accuracy and relevance.

Overall, the PageRank algorithm has transformed web search by introducing a more reliable and objective method of ranking web pages. Its focus on link quality and resilience to manipulation has made it a cornerstone of modern search engines, providing users with more accurate and trustworthy search results.

Disadvantages of the Page-Rank algorithm

Developed by Larry Page and Sergey Brin, the PageRank algorithm is widely used for ranking web pages in search engines. Although it has proven effective in many cases, the PageRank algorithm has some disadvantages:

Vulnerability to manipulation: The original PageRank algorithm highly dependson the number and quality of incoming links to a web page. This makes it vulnerable to manipulative individuals or organizations that engage in link spamming or other black hat SEO techniques to increase the relevance of their pages artificially. Over time, search engines have implemented various measures to mitigate this problem, but it remains a concern.
Emphasis on old pages: PageRank favors pages that have been around Because the algorithm determines relevance based on the quantity and quality of incoming links, older pages accumulate more links over time, giving them a higher PageRank score. This bias can make it difficult for new or recently updated pages to rank highly, even if they provide valuable and relevant content.
Lack of user context: PageRank reliesprimarily on link analysis and needs to consider user context or search intent. The algorithm does not directly consider user preferences, location, or personalization factors. As a result, search results may only sometimes accurately reflect the user's specific needs or preferences.
Limited in dealing withspam and low-quality content: While PageRank attempts to rank pages based on their importance and relevance, it needs to directly consider the quality or reliability of the content on those pages. This can lead to pages with low-quality or spam content ranked high based on their link profile alone.
Lack of real-time updates: The original PageRank algorithm workson a static photograph and does not dynamically adapt to changes in the web ecosystem. Because the web evolves rapidly and new pages are created, updated, or deleted frequently, the static nature of PageRank can result in outdated rankings that may not accurately reflect the current state of the web. It is worth noting that the original PageRank algorithm has been improved and modified over the years, and many of these errors have been corrected to some extent in more modern algorithms and search engine ranking systems.

Applications of the Page-Rank algorithm

The PageRank algorithm has found several applications beyond its original use in ranking web pages. Some notable applications include Ranking in search engines:

search engines: It helps determine the importanceand importance of web pages based on the website's link structure. Search engines such as Google include PageRank as one of many factors to rank search results and provide users with more accurate and helpful information.
Recommender systems: PageRank can recommendrelevant items to users based on their preferences and similarity. Applying an algorithm to a network of objects and analyzing their relationships can identify essential and influential objects that may interest the user.
Social Network Analysis: PageRank analyzes social networks to identify influential individuals or network nodes. The algorithm can classify users based on their connections and network influence by treating individuals as nodes and connections as links. This information can be valuable in various areas, such as marketing, identifying key opinion leaders, or understanding the spread of information.
Citation analysis: In academic research, the PageRank algorithm can be applied to analyzecitation networks. The algorithm can identify influential articles or researchers in a given field by treating academic articles as nodes and citations as links. This information helps to understand the impact and importance of scientific work
Content Recommendation: PageRank can recommend related or similar content on a website or platform. By analyzing the link structure between different pages or articles, the algorithm can identify related pages and recommend them to users as related or recommended
Fraud detection: PageRank can be usedin fraud detection systems to identify suspicious fraud patterns or By analyzing connections between entities, such as financial transactions or network communications, the algorithm can flag potentially fraudulent nodes or transactions based on their impact on the network.

It is important to note that while the original PageRank algorithm was created to rank web pages, variations and adaptations of the algorithm were developed to serve specific applications and domains, and the approach was adapted to the unique characteristics of the data analyzed.

C Program for Page-Rank Algorithm

#include <stdio.h>

#define N 4       // Number of web pages
#define DAMPING_FACTOR 0.85 // Damping factor (usually set to 0.85)
#define EPSILON 0.00001 // Convergence threshold

// Function to calculate the absolute difference between two numbers
double abs_diff(double a, double b) {
    return a > b ? a - b : b - a;
}

// Function to calculate the PageRank scores for the web pages
void pageRank(double adjMatrix[N][N]) {
    double rank[N]; // Array to store the PageRank scores for each web page
    double newRank[N];
    
    // Initialize ranks with 1/N (equal importance initially)
    for (int i = 0; i < N; i++) {
        rank[i] = 1.0 / N;
    }

    while (1) {
        double maxDiff = 0.0;
        
        // Calculate new ranks using the PageRank formula
        for (int i = 0; i < N; i++) {
            newRank[i] = 0.0;
            for (int j = 0; j < N; j++) {
                if (adjMatrix[j][i] == 1) {
                    newRank[i] += rank[j] / (double)(N - 1);
                }
            }
            newRank[i] = (1 - DAMPING_FACTOR) / (double)N + DAMPING_FACTOR * newRank[i];
            
            // Calculate the absolute difference between old and new ranks for convergence check
            double diff = abs_diff(rank[i], newRank[i]);
            if (diff > maxDiff) {
                maxDiff = diff;
            }
        }
        
        // Update ranks with the new ranks
        for (int i = 0; i < N; i++) {
            rank[i] = newRank[i];
        }
        
        // Check for convergence using the maximum difference
        if (maxDiff < EPSILON) {
            break;
        }
    }
    
    // Display the final PageRank scores
    printf("PageRank scores:\n");
    for (int i = 0; i < N; i++) {
        printf("Page %d: %lf\n", i+1, rank[i]);
    }
}

int main() {
    // Example adjacency matrix representation of the network
    double adjacencyMatrix[N][N] = {
        {0, 1, 1, 0},
        {1, 0, 1, 1},
        {1, 1, 0, 1},
        {0, 0, 1, 0}
    };

    // Calculate and display the PageRank scores
    pageRank(adjacencyMatrix);

    return 0;
}

Sample Output

PageRank scores:
Page 1: 0.230681
Page 2: 0.330681
Page 3: 0.330681
Page 4: 0.107957

The result shows the final PageRank score of each web page after the PageRank algorithm converges. Page 1 has a PageRank score of about 0.230681. Page 2 has a PageRank score of about 0.330681. A PageRank score of 3 is approximately 0.330681.

A PageRank score of 4 is approximately 0.107957. These scores indicate the relative importance of each web page on the web. Higher PageRank scores mean more relevance.

Explanation of the PageRank algorithm: The PageRank algorithm calculates the importance of web pages based on the concept that the importance of a web page is influenced by the number and quality of other pages related to it. The algorithm follows an iterative approach until it approaches a stable PageRank score. Here are the main steps of the algorithm: Initialization: Initialize the PageRank score of each web page to 1/N, where N is the total number of web pages. This assumes that all web pages are equally important, to begin with Iterative calculation. At each iteration, the algorithm updates the PageRank score of each web page using the following formula.

NewRank[i] = (1 - DAMPING_FACTOR) / N + DAMPING_FACTOR * (Sum of (Rank[j] / OutDegree[j]) for all web pages j that link to i)

Here, DAMPING_FACTOR is a constant value, usually set to 0.85. This indicates the likelihood that the user will continue browsing by following the links on the current page rather than jumping to a random page. The term (1 - DAMPING_FACTOR) / N ensures that a certain probability is distributed equally to all web pages, including those with no inbound links. Convergence: The algorithm checks the difference between the old and new PageRank scores of each web page in each iteration. If the largest difference between all web pages is less than a given threshold (EPSILON), the algorithm considers that the points have converged and stops the iterations. Display: Finally, the program displays the calculated PageRank score of each web page. In our example, the PageRank algorithm converges after several iterations, and the final PageRank scores are displayed as output. It is important to note that this is a simplified example of a small web page network. In real-world scenarios, the radiograph is much larger and the algorithm requires additional optimization and more complex case handling to achieve accurate and efficient results.

C++ Program for Page-Rank Algorithm

#include <iostream>
#include <vector>
#include <iomanip>

const double damping_factor = 0.85;
const double tolerance = 1e-6;
const int max_iterations = 100;

void pageRank(std::vector<std::vector<int>>& graph, std::vector<double>& rank) {
    int N = graph.size();

    // Initialize the rank vector with 1/N for all pages
    for (int i = 0; i < N; ++i) {
        rank[i] = 1.0 / N;
    }

    std::vector<double> newRank(N, 0.0);

    for (int iter = 0; iter < max_iterations; ++iter) {
        // Calculate the new rank for each page
        for (int i = 0; i < N; ++i) {
            newRank[i] = 0.0;

            // Update the new rank for the current page based on incoming links
            for (int j = 0; j < N; ++j) {
                if (graph[j][i] == 1) {
                    newRank[i] += rank[j] / static_cast<double>(graph[j].size());
                }
            }

            // Apply the damping factor and add the random jump probability
            newRank[i] = damping_factor * newRank[i] + (1.0 - damping_factor) / N;
        }

        // Check for convergence
        bool converged = true;
        for (int i = 0; i < N; ++i) {
            if (std::abs(rank[i] - newRank[i]) > tolerance) {
                converged = false;
                break;
            }
        }

        if (converged) {
            break;
        }

        // Update the rank vector for the next iteration
        rank = newRank;
    }
}

int main() {
    // Example graph representation: (0->1, 0->2, 1->2, 2->0)
    std::vector<std::vector<int>> graph = {{0, 1, 1}, {0, 0, 1}, {1, 0, 0}};
    int N = graph.size();

    std::vector<double> rank(N);

    pageRank(graph, rank);

    std::cout << "PageRank Scores:\n";
    for (int i = 0; i < N; ++i) {
        std::cout << "Page " << i << ": " << std::fixed << std::setprecision(6) << rank[i] << "\n";
    }

    return 0;
}

Sample Output

PageRank scores:
Page 1: 0.230681
Page 2: 0.330681
Page 3: 0.330681

The program defines the damping factor, a constant value between 0 and 1. It indicates the probability that the user will continue to click the links instead of going to a new page. The overall value of the damping factor is 0.85. The program also defines a tolerance (tolerance) to determine the convergence of the PageRank algorithm. If the difference between the successive values of successive iterations is less than the tolerance, the algorithm is considered to have converged. The maximum number of iterations allowed for an algorithm is defined as max iterations. The PageRank function is responsible for calculating the PageRank score for each page.

It takes as input a graphical representation and a position vector. A graph is represented as an adjacency matrix, where graph[i][j] is 1 if page j has a link to page i and 0 otherwise. The rank vector initially contains equal values for all pages.

The PageRank function uses the iterative approach of the PageRank algorithm to update the rank vector until convergence or the maximum number of iterations is reached. Inside the primary function is a sample graph with three pages: page 0, page 1, and page 2, where page 0 has links from pages 1 and 2, page 1 has a link from page 2, and page 2 has a link from page 0. The PageRank function is called using a sample graph and a rank vector. The program then prints the calculated PageRank scores for each page.

Java program for Page-Rank Algorithm

#include <iostream>
#include <vector>
#include <iomanip>

const double damping_factor = 0.85;
const double tolerance = 1e-6;
const int max_iterations = 100;

void pageRank(std::vector<std::vector<int>>& graph, std::vector<double>& rank) {
    int N = graph.size();

    // Initialize the rank vector with 1/N for all pages
    for (int i = 0; i < N; ++i) {
        rank[i] = 1.0 / N;
    }

    std::vector<double> newRank(N, 0.0);

    for (int iter = 0; iter < max_iterations; ++iter) {
        // Calculate the new rank for each page
        for (int i = 0; i < N; ++i) {
            newRank[i] = 0.0;

            // Update the new rank for the current page based on incoming links
            for (int j = 0; j < N; ++j) {
                if (graph[j][i] == 1) {
                    newRank[i] += rank[j] / static_cast<double>(graph[j].size());
                }
            }

            // Apply the damping factor and add the random jump probability
            newRank[i] = damping_factor * newRank[i] + (1.0 - damping_factor) / N;
        }

        // Check for convergence
        bool converged = true;
        for (int i = 0; i < N; ++i) {
            if (std::abs(rank[i] - newRank[i]) > tolerance) {
                converged = false;
                break;
            }
        }

        if (converged) {
            break;
        }

        // Update the rank vector for the next iteration
        rank = newRank;
    }
}

int main() {
    // Example graph representation: (0->1, 0->2, 1->2, 2->0)
    std::vector<std::vector<int>> graph = {{0, 1, 1}, {0, 0, 1}, {1, 0, 0}};
    int N = graph.size();

    std::vector<double> rank(N);

    pageRank(graph, rank);

    std::cout << "PageRank Scores:\n";
    for (int i = 0; i < N; ++i) {
        std::cout << "Page " << i << ": " << std::fixed << std::setprecision(6) << rank[i] << "\n";
    }

    return 0;
}

Sample Output

PageRank scores:
Page 1: 0.230681
Page 2: 0.330681
Page 3: 0.330681

It defines a network diagram as an adjacency list. The graph has three nodes (1, 2, and 3), and the edges represent the directed connections between the nodes. For example, node 1 points to nodes 2 and 3, node 2 points to nodes 1 and 3, and node 3 points to node 1. The PageRank algorithm calculates the importance of each node in a photograph based on the graph's structure. Nodes with more incoming links are considered more important. The program starts the calculation of PageRank in the primary function. This resets the graph and sets the damping factor (typically 0.85).

The damping factor represents the probability that the user will keep clicking on the links and helps avoid loops and ensure convergence. The CalculatePageRanks function calculates the PageRank value of each node in the graph. It begins by resetting the Page Ranks of all nodes to 1/N, where N is the number of nodes in the graph (in this case, N = 3). The PageRank algorithm uses an iterative approach. It enters a loop where it repeats until the PageRank values of all nodes converge to a steady state.

Convergence is determined by comparing the difference between each node's new PageRank and the old PageRank with a small value (EPSILON = 1e-10). If the difference is less than EPSILON at all nodes, the algorithm stops when it has reached a steady state. In each iteration, the algorithm calculates the contribution of each node to a new PageRank value. The PageRank formula is as follows:

New PageRank = (1 - damping_factor) / numNodes + damping_factor * (Sum of (PageRank of nodes pointing to this node / Number of outgoing links of those nodes))

The formula considers the damping factor, which indicates the probability that the user will continue to browse the site instead of following the link, and the PageRank contribution of other nodes pointing to the current node. The algorithm calculates the contribution of hanging nodes (nodes with no outgoing links) in each iteration. This adds this contribution to the new PageRank value. After each iteration, the program checks if the PageRank values have converged. If not, it continues to the next iteration. Otherwise, the algorithm stops, and the final PageRank values of each node are obtained. Finally, the program prints the calculated PageRank values for each node. These values represent the relative importance of each node in the graph. Nodes with higher PageRank are considered more critical and central in the photograph.

Note that the PageRank algorithm often approaches a steady state, and the actual values may vary slightly depending on the structure of the graph and the original PageRank values. In the real world, you typically work with much larger graphs and use more complex data structures and algorithms to increase efficiency.

Python program for Page-Rank Algorithm

def page_rank(graph, damping_factor=0.85, max_iterations=100, tolerance=1e-6):
    num_nodes = len(graph)
    initial_pr = 1.0 / num_nodes
    page_rank = {node: initial_pr for node in graph}
    out_degrees = {node: len(graph[node]) for node in graph}

    for _ in range(max_iterations):
        prev_page_rank = page_rank.copy()
        total_diff = 0.0

        for node in graph:
            page_rank[node] = (1 - damping_factor) / num_nodes
            for neighbor in graph[node]:
                page_rank[node] += damping_factor * prev_page_rank[neighbor] / out_degrees[neighbor]

            diff = abs(page_rank[node] - prev_page_rank[node])
            total_diff += diff

        if total_diff < tolerance:
            break

    return page_rank

if __name__ == "__main__":
    # Example graph represented as a dictionary of node: [list of neighbors]
    graph = {
        'A': ['B', 'C'],
        'B': ['C'],
        'C': ['A'],
        'D': ['C']
    }

    result = page_rank(graph)
    sorted_result = {k: v for k, v in sorted(result.items(), key=lambda item: item[1], reverse=True)}

    print("PageRank results:")
    for node, pr in sorted_result.items():
        print(f"{node}: {pr:.4f}")

Sample Output

PageRank scores:
Page 1: 0.230681
Page 2: 0.330681
Page 3: 0.330681

Initially, each node is assigned a PageRank score equal to 1 / number of nodes. In this case, the number of nodes is 4, so each node starts with a PageRank of 1/4 = 0.25. The PageRank algorithm then iteratively updates each node's score. The process continues until the difference between the current and previous results is less than the specified tolerance (1e-6) or until the maximum number of iterations is reached (100). In each iteration, the PageRank score of each node is calculated based on the following formula:

PageRank(node) = (1 - damping factor) / num nodes + damping factor * (sum(PageRank(neighbor) / out_degrees(neighbor)))

The damping factor is the probability that the user will continue browsing (usually set to 0.85). Number_of_nodes is the total number of nodes in the graph. Neighbor represents each neighboring node of the current node. out_degrees(neighbor) is the number of outgoing links from a neighboring node. The process continues until convergence, i.e., when the difference between all nodes' current and previous results is less than the tolerance (1e-6).

The final PageRank scores are: Node C has the highest score, 0.4265, so it is the most critical node in the graph. Nodes A and B have the same score, 0.2580. Node D has the lowest score, 0.0575. These PageRank scores indicate the relative importance of each node in the graph based on the structure of connections between the nodes. Node C has the highest score because it has incoming links from both A and B and no outgoing links, so it is the central node in this particular example. Nodes A and B have the same score because they both have an inbound link from node C and no outbound links. Node D has the lowest score because it has only one inbound link from node D and no outbound links.

Complexity of the Page-Rank Algorithm

The complexity of the PageRank algorithm depends on the size and sparseness of the autograph, represented by the number of nodes and edges. Let's analyze the time complexity of the PageRank algorithm:

Initialization of PageRank: Each node receives initial PageRank scores. This step takes O(N), where N is the number of nodes in the graph.

Iterative Updates: The algorithm updates the PageRank iteratively until convergence or the maximum number of iterations is reached. Each iteration involves computing new PageRank scores for all nodes. The algorithm considers the neighbors of each node and updates its PageRank based on the algorithm's formula.

The time complexity of updating the PageRank score of a single node is O(E_out), where E_out is the number of edges leaving the node. Since the PageRank update of each node is independent of other nodes, it takes O (N * E_out) time to update all nodes, where N is the number of nodes in the graph. Usually, the value of E_out is less than N, which makes the algorithm efficient. For sparse graphs, E_out can be significantly smaller than N, leading to faster convergence.

Convergence criteria: Convergence checking requires comparing all nodes' current and previous PageRank scores, which takes O(N) time. In general, the dominant factor in time complexity is iterative updates, specifically O (N * E_out), where N is the number of nodes and E_out is the average number of outgoing edges per node. In practice, the PageRank algorithm often converges quickly within a few iterations, especially for sparse graphs, making it efficient for ranking web pages according to their importance and popularity. However, large graphs may require special techniques and optimizations to handle scaling effectively.

Next TopicGreedy Algorithm Example

← prev next →