Subset CoverTo Prove:-
1) Subset CoverDefinition: - Number of a subset of edges after making the union for a get all the edges of the complete graph G, and that is called Subset Cover. According to the graph G, which you have created the size of Subset Cover=2 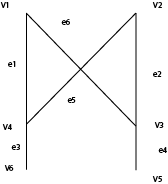
2) Vertex Cover ≤ρ Subset CoverIn a graph G of vertices N, if there exists a Vertex Cover of size k, then there must also exist a Subset Cover of size k even. If you can achieve after the Reduction from Vertex Cover to Subset Cover within a polynomial time, which means you did right. 3) Subset Cover ≤ρ Vertex CoverJust for verification of the output perform the Reduction and create Clique and via an equation, N-K verifies the Clique also and through Clique you can quickly generate 3CNF and after solving the Boolean function of 3CNF in the polynomial time. You will get output. It means the output has been verified. 4) Subset Cover ϵ NP:-Proof: - As you know very well, you can get the Subset-Cover through Vertex Cover and Vertex Cover through Clique and to convert the decision-based NP problem into Clique firstly you have to convert into3CNF and 3CNF into SAT and SAT into CIRCUIT SAT that comes from NP. Proof of NPC:- The Reduction has been successfully made within the polynomial time form Vertex Cover to Subset Cover Output has also been verified within the polynomial time as you did in the above conversation so, concluded that SUBSET COVER also comes in NPC. Independent Set:An independent set of a graph G = (V, E) is a subset V'⊆V of vertices such that every edge in E is incident on at most one vertex in V.' The independent-set problem is to find a largest-size independent set in G. It is not hard to find small independent sets, e.g., a small independent set is an individual node, but it is hard to find large independent sets. 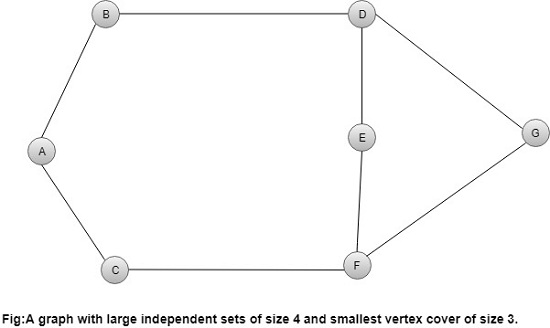
Next TopicApproximation Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










