Dijkstra's Algorithm

The following tutorial will teach us about Dijkstra's Shortest Path Algorithm. We will understand the working of Dijkstra's Algorithm with a stepwise graphical explanation.

We will cover the following:

• A Brief Overview of the Fundamental Concepts of Graph
• Understand the Use of Dijkstra's Algorithm
• Understand the Working of the Algorithm with a Step-by-Step Example

So, let's get started.

A Brief Introduction to Graphs

Graphs are non-linear data structures representing the "connections" between the elements. These elements are known as the Vertices, and the lines or arcs that connect any two vertices in the graph are known as the Edges. More formally, a Graph comprises a set of Vertices (V) and a set of Edges (E). The Graph is denoted by G(V, E).

Components of a Graph

1. Vertices:Vertices are the basic units of the graph used to represent real-life objects, persons, or entities. Sometimes, vertices are also known as Nodes.
2. Edges:Edges are drawn or used to connect two vertices of the graph. Sometimes, edges are also known as Arcs.

The following figure shows a graphical representation of a Graph: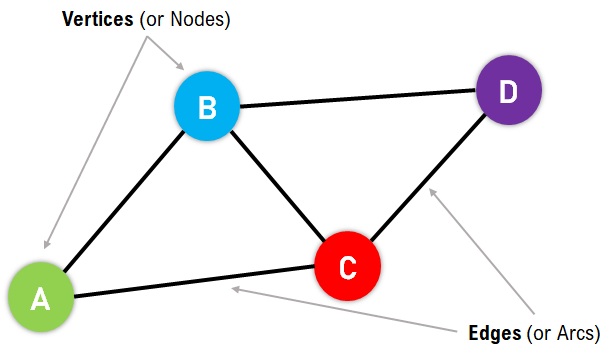

Figure 1: Graphical Representation of a Graph

In the above figure, the Vertices/Nodes are denoted with Colored Circles, and the Edges are denoted with the lines connecting the nodes.

Applications of the Graphs

Graphs are used to solve many real-life problems. Graphs are utilized to represent the networks. These networks may include telephone or circuit networks or paths in a city.

For example, we could use Graphs to design a transportation network model where the vertices display the facilities that send or receive the products, and the edges represent roads or paths connecting them. The following is a pictorial representation of the same: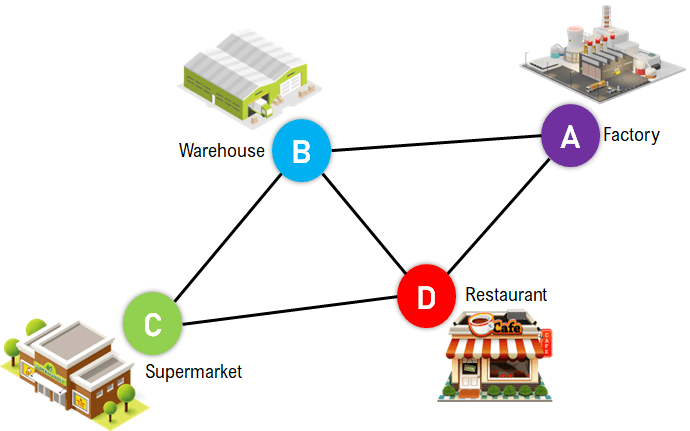

Figure 2: Pictorial Representation of Transportation Network

Graphs are also utilized in different Social Media Platforms like LinkedIn, Facebook, Twitter, and more. For example, Platforms like Facebook use Graphs to store the data of their users where every person is indicated with a vertex, and each of them is a structure containing information like Person ID, Name, Gender, Address, etc.

Types of Graphs

The Graphs can be categorized into two types:

1. Undirected Graph
2. Directed Graph

Undirected Graph: A Graph with edges that do not have a direction is termed an Undirected Graph. The edges of this graph imply a two-way relationship in which each edge can be traversed in both directions. The following figure displays a simple undirected graph with four nodes and five edges.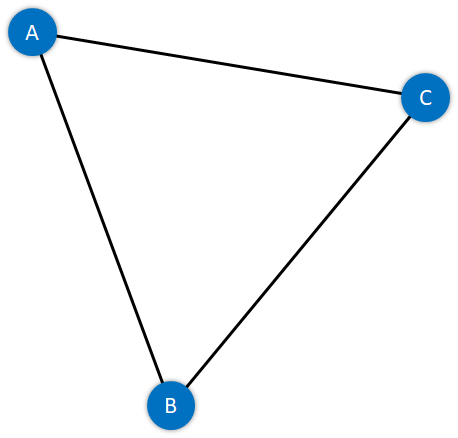

Figure 3: A Simple Undirected Graph

Directed Graph: A Graph with edges with direction is termed a Directed Graph. The edges of this graph imply a one-way relationship in which each edge can only be traversed in a single direction. The following figure displays a simple directed graph with four nodes and five edges.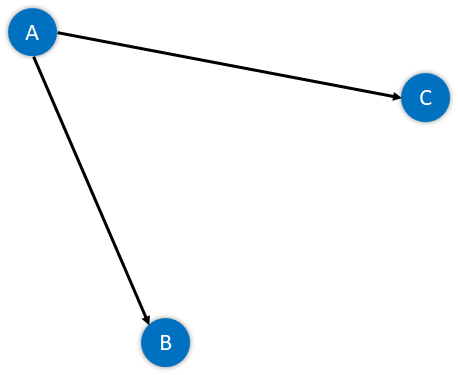

Figure 4: A Simple Directed Graph

The absolute length, position, or orientation of the edges in a graph illustration characteristically does not have meaning. In other words, we can visualize the same graph in different ways by rearranging the vertices or distorting the edges if the underlying structure of the graph does not alter.

What are Weighted Graphs?

A Graph is said to be Weighted if each edge is assigned a 'weight'. The weight of an edge can denote distance, time, or anything that models the 'connection' between the pair of vertices it connects.

For instance, we can observe a blue number next to each edge in the following figure of the Weighted Graph. This number is utilized to signify the weight of the corresponding edge.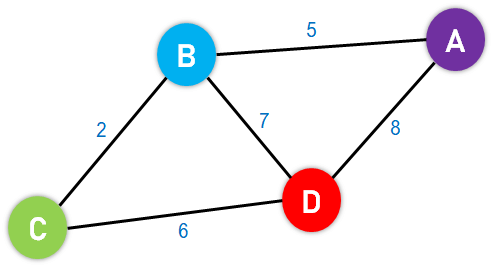

Figure 5: An Example of a Weighted Graph

An Introduction to Dijkstra's Algorithm

Now that we know some basic Graphs concepts let's dive into understanding the concept of Dijkstra's Algorithm.

Ever wondered how does Google Maps finds the shortest and fastest route between two places?

Well, the answer is Dijkstra's Algorithm. Dijkstra's Algorithm is a Graph algorithm that finds the shortest path from a source vertex to all other vertices in the Graph (single source shortest path). It is a type of Greedy Algorithm that only works on Weighted Graphs having positive weights. The time complexity of Dijkstra's Algorithm is O(V²) with the help of the adjacency matrix representation of the graph. This time complexity can be reduced to O((V + E) log V) with the help of an adjacency list representation of the graph, where V is the number of vertices and E is the number of edges in the graph.

History of Dijkstra's Algorithm

Dijkstra's Algorithm was designed and published by Dr. Edsger W. Dijkstra, a Dutch Computer Scientist, Software Engineer, Programmer, Science Essayist, and Systems Scientist.

During an Interview with Philip L. Frana for the Communications of the ACM journal in the year 2001, Dr. Edsger W. Dijkstra revealed:

"What is the shortest way to travel from Rotterdam to Groningen, in general: from given city to given city? It is the algorithm for the shortest path, which I designed in about twenty minutes. One morning I was shopping in Amsterdam with my young fiancée, and tired, we sat down on the café terrace to drink a cup of coffee and I was just thinking about whether I could do this, and I then designed the algorithm for the shortest path. As I said, it was a twenty-minute invention. In fact, it was published in '59, three years later. The publication is still readable, it is, in fact, quite nice. One of the reasons that it is so nice was that I designed it without pencil and paper. I learned later that one of the advantages of designing without pencil and paper is that you are almost forced to avoid all avoidable complexities. Eventually, that algorithm became to my great amazement, one of the cornerstones of my fame."

Dijkstra thought about the shortest path problem while working as a programmer at the Mathematical Centre in Amsterdam in 1956 to illustrate the capabilities of a new computer known as ARMAC. His goal was to select both a problem and a solution (produced by the computer) that people with no computer background could comprehend. He developed the shortest path algorithm and later executed it for ARMAC for a vaguely shortened transportation map of 64 cities in the Netherlands (64 cities, so 6 bits would be sufficient to encode the city number). A year later, he came across another issue from hardware engineers operating the next computer of the institute: Minimize the amount of wire required to connect the pins on the machine's back panel. As a solution, he re-discovered the algorithm called Prim's minimal spanning tree algorithm and published it in the year 1959.

Fundamentals of Dijkstra's Algorithm

The following are the basic concepts of Dijkstra's Algorithm:

1. Dijkstra's Algorithm begins at the node we select (the source node), and it examines the graph to find the shortest path between that node and all the other nodes in the graph.
2. The Algorithm keeps records of the presently acknowledged shortest distance from each node to the source node, and it updates these values if it finds any shorter path.
3. Once the Algorithm has retrieved the shortest path between the source and another node, that node is marked as 'visited' and included in the path.
4. The procedure continues until all the nodes in the graph have been included in the path. In this manner, we have a path connecting the source node to all other nodes, following the shortest possible path to reach each node.

Understanding the Working of Dijkstra's Algorithm

A graph and source vertex are requirements for Dijkstra's Algorithm. This Algorithm is established on Greedy Approach and thus finds the locally optimal choice (local minima in this case) at each step of the Algorithm.

Each Vertex in this Algorithm will have two properties defined for it:

1. Visited Property
2. Path Property

Let us understand these properties in brief.

Visited Property:

1. The 'visited' property signifies whether or not the node has been visited.
2. We are using this property so that we do not revisit any node.
3. A node is marked visited only when the shortest path has been found.

Path Property:

1. The 'path' property stores the value of the current minimum path to the node.
2. The current minimum path implies the shortest way we have reached this node till now.
3. This property is revised when any neighbor of the node is visited.
4. This property is significant because it will store the final answer for each node.

Initially, we mark all the vertices, or nodes, unvisited as they have yet to be visited. The path to all the nodes is also set to infinity apart from the source node. Moreover, the path to the source node is set to zero (0).

We then select the source node and mark it as visited. After that, we access all the neighboring nodes of the source node and perform relaxation on every node. Relaxation is the process of lowering the cost of reaching a node with the help of another node.

In the process of relaxation, the path of each node is revised to the minimum value amongst the node's current path, the sum of the path to the previous node, and the path from the previous node to the current node.

Let us suppose that p[n] is the value of the current path for node n, p[m] is the value of the path up to the previously visited node m, and w is the weight of the edge between the current node and previously visited one (edge weight between n and m).

In the mathematical sense, relaxation can be exemplified as:

p[n] = minimum(p[n], p[m] + w)

We then mark an unvisited node with the least path as visited in every subsequent step and update its neighbor's paths.

We repeat this procedure until all the nodes in the graph are marked visited.

Whenever we add a node to the visited set, the path to all its neighboring nodes also changes accordingly.

If any node is left unreachable (disconnected component), its path remains 'infinity'. In case the source itself is a separate component, then the path to all other nodes remains 'infinity'.

Understanding Dijkstra's Algorithm with an Example

The following is the step that we will follow to implement Dijkstra's Algorithm:

Step 1: First, we will mark the source node with a current distance of 0 and set the rest of the nodes to INFINITY.

Step 2: We will then set the unvisited node with the smallest current distance as the current node, suppose X.

Step 3: For each neighbor N of the current node X: We will then add the current distance of X with the weight of the edge joining X-N. If it is smaller than the current distance of N, set it as the new current distance of N.

Step 4: We will then mark the current node X as visited.

Step 5: We will repeat the process from 'Step 2' if there is any node unvisited left in the graph.

Let us now understand the implementation of the algorithm with the help of an example: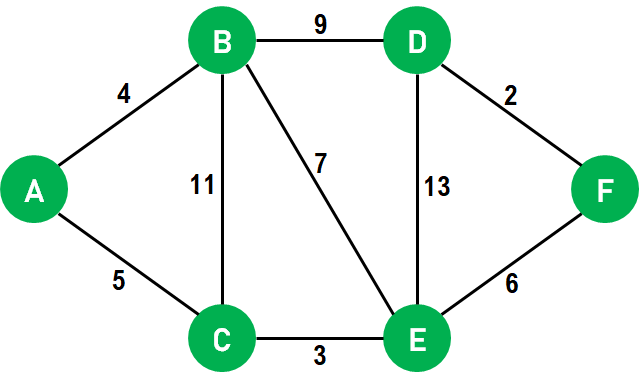

Figure 6: The Given Graph

1. We will use the above graph as the input, with node A as the source.
2. First, we will mark all the nodes as unvisited.
3. We will set the path to 0 at node A and INFINITY for all the other nodes.
4. We will now mark source node A as visited and access its neighboring nodes.
   Note: We have only accessed the neighboring nodes, not visited them.
5. We will now update the path to node B by 4 with the help of relaxation because the path to node A is 0 and the path from node A to B is 4, and the minimum((0 + 4), INFINITY) is 4.
6. We will also update the path to node C by 5 with the help of relaxation because the path to node A is 0 and the path from node A to C is 5, and the minimum((0 + 5), INFINITY) is 5. Both the neighbors of node A are now relaxed; therefore, we can move ahead.
7. We will now select the next unvisited node with the least path and visit it. Hence, we will visit node B and perform relaxation on its unvisited neighbors. After performing relaxation, the path to node C will remain 5, whereas the path to node E will become 11, and the path to node D will become 13.
8. We will now visit node E and perform relaxation on its neighboring nodes B, D, and F. Since only node F is unvisited, it will be relaxed. Thus, the path to node B will remain as it is, i.e., 4, the path to node D will also remain 13, and the path to node F will become 14 (8 + 6).
9. Now we will visit node D, and only node F will be relaxed. However, the path to node F will remain unchanged, i.e., 14.
10. Since only node F is remaining, we will visit it but not perform any relaxation as all its neighboring nodes are already visited.
11. Once all the nodes of the graphs are visited, the program will end.

Hence, the final paths we concluded are:

Pseudocode for Dijkstra's Algorithm

We will now understand a pseudocode for Dijkstra's Algorithm.

• We have to maintain a record of the path distance of every node. Therefore, we can store the path distance of each node in an array of size n, where n is the total number of nodes.
• Moreover, we want to retrieve the shortest path along with the length of that path. To overcome this problem, we will map each node to the node that last updated its path length.
• Once the algorithm is complete, we can backtrack the destination node to the source node to retrieve the path.
• We can use a minimum Priority Queue to retrieve the node with the least path distance in an efficient way.

Let us now implement a pseudocode of the above illustration:

Pseudocode:

Explanation:

In the above pseudocode, we have defined a function that accepts multiple parameters - the Graph consisting of the nodes and the source node. Inside this function, we have iterated through each node in the Graph, set their initial distance to INFINITY, and set the previous node value to NULL. We have also checked whether any selected node is not a source node and added the same into the Priority Queue. Moreover, we have set the distance of the source node to 0. We then iterated through the nodes in the priority queue, selected the node with the least distance, and marked it as visited. We then iterated through the unvisited neighboring nodes of the selected node and performed relaxation accordingly. At last, we have compared both the distances (original and temporary distance) between the source node and the destination node, updated the resultant distance with the minimum value and previous node information, and returned the final list of distances with their previous node information.

Implementation of Dijkstra's Algorithm in Different Programming Languages

Now that we have successfully understood the pseudocode of Dijkstra's Algorithm, it is time to see its implementation in different programming languages like C, C++, Java, and Python.

Code for Dijkstra's Algorithm in C

The following is the implementation of Dijkstra's Algorithm in the C Programming Language:

File: DijkstraAlgorithm.c

Output

Distance from the Source Node to 1: 4
Distance from the Source Node to 2: 12
Distance from the Source Node to 3: 19
Distance from the Source Node to 4: 12
Distance from the Source Node to 5: 8
Distance from the Source Node to 6: 10

Explanation:

In the above snippet of code, we have included the stdio.h header file defined two constant values: INF = 9999 and MAX = 10. We have declared the prototyping of the function and then defined the function for Dijkstra's Algorithm as DijkstraAlgorithm that accepts three arguments - the Graph consisting of the nodes, the number of nodes in the Graph, and the source node. Inside this function, we have defined some data structures such as a 2D matrix that will work as the Priority Queue for the algorithm, an array to main the distance between the nodes, an array to maintain the record of previous nodes, an array to store the visited nodes information, and some integer variables to store minimum distance value, counter, next node value and more. We then used a nested for-loop to iterate through the nodes of the Graph and add them to the priority queue accordingly. We have again used the for-loop to iterate through the elements in the priority queue starting from the source node and update their distances. Outside the loop, we have set the distance of the source node as 0 and marked it as visited in the visited_nodes[] array. We then set the counter value as one and used the while loop iterating through the number of nodes. Inside this loop, we have set the value of minimum_distance as INF and used the for-loop to update the value of the minimum_distance variable with the minimum value from a distance[] array. We then iterated through the unvisited neighboring nodes of the selected node using the for-loop and performed relaxation. We then printed the resulting data of the distances calculated using Dijkstra's Algorithm.

In the main function, we have defined and declared the variables representing the Graph, the number of nodes, and the source node. At last, we have called the DijkstraAlgorithm() function by passing the required parameters.

As a result, the required shortest possible paths for every node from the source node are printed for the users.

Code for Dijkstra's Algorithm in C++

The following is the implementation of Dijkstra's Algorithm in the C++ Programming Language:

File: DijkstraAlgorithm.cpp

Output

Distance from start: 4
F G D A

Explanation:

In the above code snippet, we included the 'iostream' and 'vector' header files and defined a constant value as MAX_INT = 10000000. We then used the standard namespace and prototyped the DijkstraAlgorithm() function. We then defined the main function of the program within, which we have called the DijkstraAlgorithm() function. After that, we declared some classes to create vertices and edges. We have also prototyped more functions to find the shortest possible path from the source vertex to the destination vertex and instantiated the Vertex and Edge classes. We then defined both classes to create the vertices and edges of the graph. We have then defined the DijkstraAlgorithm() function to create a graph and perform different operations. Inside this function, we have declared some vertices and edges. We then set the source vertex of the graph and called the Dijkstra() function to find the shortest possible distance and Print_Shortest_Route_To() function to print the shortest distance from the source vertex to vertex 'F'. We have then defined the Dijkstra() function to calculate the shortest possible distances of the all the vertices from the source vertex. We have also defined some more functions to find the vertex with the shortest distance to return all the vertices adjacent to the remaining vertex, to return the distance between two connected vertices, to check if the selected vertex exists in the graph, and to print the shortest possible path from the source vertex to the destination vertex.

As a result, the required shortest path for the vertex 'F' from the source node is printed for the users.

Code for Dijkstra's Algorithm in Java

The following is the implementation of Dijkstra's Algorithm in the Java Programming Language:

File: DijkstraAlgorithm.java

Output

Distance from Vertex 0 to Vertex 0 is 0
Distance from Vertex 0 to Vertex 1 is 1
Distance from Vertex 0 to Vertex 2 is 1
Distance from Vertex 0 to Vertex 3 is 2
Distance from Vertex 0 to Vertex 4 is 4
Distance from Vertex 0 to Vertex 5 is 4
Distance from Vertex 0 to Vertex 6 is 3

Explanation:

In the above snippet of code, we have defined a public class as DijkstraAlgorithm(). Inside this class, we have defined a public method as dijkstraAlgorithm() to find the shortest distance from the source vertex to the destination vertex. Inside this method, we have defined a variable to store the number of nodes. We have then defined a Boolean array to store the information regarding the visited vertices and an integer array to store their respective distances. Initially, we declared the values in both the arrays as False and MAX_VALUE, respectively. We have also set the distance of the source vertex as zero and used the for-loop to update the distance between the source vertex and destination vertices with the minimum distance. We have then updated the distances of the neighboring vertices of the selected vertex by performing relaxation and printed the shortest distances for every vertex. We have then defined a method to find the minimum distance from the source vertex to the destination vertex. We then defined the main function where we declared the vertices of the graph and instantiated the DijkstraAlgorithm() class. Finally, we have called the dijkstraAlgorithm() method to find the shortest distance between the source vertex and the destination vertices.

As a result, the required shortest possible paths for every node from the source node are printed for the users.

Code for Dijkstra's Algorithm in Python

The following is the implementation of Dijkstra's Algorithm in the Python Programming Language:

File: DikstraAlgorithm.py

Output

Distance of A from source node: 0
Distance of B from source node: 3
Distance of C from source node: 1
Distance of D from source node: 2
Distance of E from source node: 2
Distance of F from source node: 4
Distance of G from source node: 3

Explanation:

In the above snippet of code, we have imported the sys module and declared the lists consisting of the values for the nodes and edges. We have then defined a function as toBeVisited() to find which node will be visited next. We then found the total number of nodes in the graph and set the initial distances for every node. We have then calculated the minimum distance from the source node to the destination node, performed relaxation on neighboring nodes, and updated the distances in the list. We then printed those distances from the list for the users.

As a result, the required shortest possible paths for every node from the source node are printed for the users.

Time and Space Complexity of Dijkstra's Algorithm

• The Time Complexity of Dijkstra's Algorithm is O(E log V), where E is the number of edges and V is the number of vertices.
• The Space Complexity of Dijkstra's Algorithm is O(V), where V is the number of vertices.

Advantages and Disadvantages of Dijkstra's Algorithm

Let us discuss some advantages of Dijkstra's Algorithm:

1. One primary advantage of using Dijkstra's Algorithm is that it has an almost linear time and space complexity.
2. We can use this algorithm to calculate the shortest path from a single vertex to all other vertices and a single source vertex to a single destination vertex by stopping the algorithm once we get the shortest distance for the destination vertex.
3. This algorithm only works for directed weighted graphs, and all the edges of this graph should be non-negative.

Despite having multiple advantages, Dijkstra's algorithm has some disadvantages also, such as:

1. Dijkstra's Algorithm performs a concealed exploration that utilizes a lot of time during the process.
2. This algorithm is impotent to handle negative edges.
3. Since this algorithm heads to the acyclic graph, it cannot calculate the exact shortest path.
4. It also requires maintenance to keep a record of vertices that have been visited.

Some Applications of Dijkstra's Algorithm

Dijkstra's Algorithm has various real-world applications, some of which are stated below:

1. Digital Mapping Services in Google Maps: There are various times when we have tried to find the distance in Google Maps either from our location to the nearest preferred location or from one city to another, which comprises multiple routes/paths connecting them; however, the application must display the minimum distance. This is only possible because Dijkstra's algorithm helps the application find the shortest between two given locations along the path. Let us consider the USA as a graph wherein the cities/places are represented as vertices, and the routes between two cities/places are represented as edges. Then with the help of Dijkstra's Algorithm, we can calculate the shortest routes between any two cities/places.
2. Social Networking Applications: In many applications like Facebook, Twitter, Instagram, and more, many of us might have observed that these apps suggest the list of friends that a specific user may know. How do many social media companies implement this type of feature in an efficient and effective way, specifically when the system has over a billion users? The answer to this question is Dijkstra's Algorithm. The standard Dijkstra's Algorithm is generally used to estimate the shortest distance between the users measured through the connections or mutuality among them. When social networking is very small, it uses the standard Dijkstra's Algorithm in addition to some other features in order to determine the shortest paths. However, when the graph is much bigger, the standard algorithm takes several seconds to count, and thus, some advanced algorithms are used as the alternative.
3. Telephone Network: As some of us might know, in a telephone network, each transmission line has a bandwidth, 'b'. The bandwidth is the highest frequency that the transmission line can support. In general, if the frequency of the signal is higher in a specific line, the signal is reduced by that line. Bandwidth represents the amount of information that can be transmitted by the line. Let us consider a city a graph wherein the switching stations are represented using the vertices, the transmission lines are represented as the edges, and the bandwidth, 'b', is represented using the weight of the edges. Thus, as we can observe, the telephone network can also fall into the category of the shortest distance problem and can be solved using Dijkstra's Algorithm.
4. Flight Program: Suppose that a person requires software to prepare an agenda of flights for customers. The agent has access to a database with all flights and airports. In addition to the flight number, origin airport, and destination, the flights also have departure and arrival times. So, in order to determine the earliest arrival time for the selected destination from the original airport and given start time, the agents make use of Dijkstra's Algorithm.
5. IP routing to find Open Shortest Path First: Open Shortest Path First (abbreviated as OSPF) is a link-state routing protocol used to find the best path between the source and destination router with the help of its own Shortest Path First. Dijkstra's Algorithm is extensively utilized in the routing protocols required by the routers in order to update their forwarding table. The algorithm gives the shortest cost path from the source router to the other routers present in the network.
6. Robotic Path: These days, drones and robots have come into existence, some operated manually and some automatically. The drones and robots which are operated automatically and used to deliver the packages to a given location or used for any certain task are configured with Dijkstra's Algorithm module so that whenever the source and destination are known, the drone and robot will move in the ordered direction by following the shortest path keeping the time taken to a minimum in order to deliver the packages.
7. Designate the File Server: Dijkstra's Algorithm is also used to designate a file server in a Local Area Network (LAN). Suppose that an infinite period of time is needed for the transmission of the files from one computer to another. So, to minimize the number of 'hops' from the file server to every other computer on the network, we will use Dijkstra's Algorithm. This algorithm will return the shortest path between the networks resulting in the minimum number of hops.

The Conclusion

• In the above tutorial, firstly, we have understood the basic concepts of Graph along with its types and applications.
• We then learned about Dijkstra's Algorithm and its history.
• We have also understood the fundamental working of Dijkstra's Algorithm with the help of an example.
• After that, we studied how to write code for Dijkstra's Algorithm with the help of Pseudocode.
• We observed its implementation in programming languages like C, C++, Java, and Python with proper outputs and explanations.
• We have also understood the Time and Space Complexity of Dijkstra's Algorithm.
• Finally, we have discussed the advantages and disadvantages of Dijkstra's algorithm and some of its real-life applications.