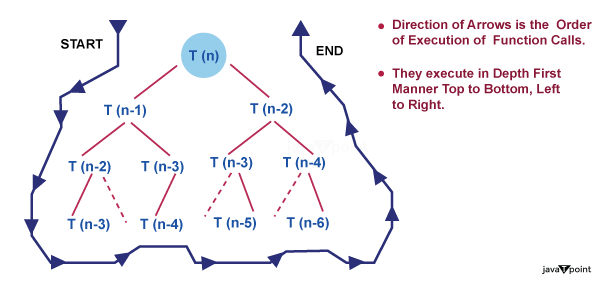
Recursion Tree Method

Recursion is a fundamental concept in computer science and mathematics that allows functions to call themselves, enabling the solution of complex problems through iterative steps. One visual representation commonly used to understand and analyze the execution of recursive functions is a recursion tree. In this article, we will explore the theory behind recursion trees, their structure, and their significance in understanding recursive algorithms.

What is a Recursion Tree?

A recursion tree is a graphical representation that illustrates the execution flow of a recursive function. It provides a visual breakdown of recursive calls, showcasing the progression of the algorithm as it branches out and eventually reaches a base case. The tree structure helps in analyzing the time complexity and understanding the recursive process involved.

Tree Structure

Each node in a recursion tree represents a particular recursive call. The initial call is depicted at the top, with subsequent calls branching out beneath it. The tree grows downward, forming a hierarchical structure. The branching factor of each node depends on the number of recursive calls made within the function. Additionally, the depth of the tree corresponds to the number of recursive calls before reaching the base case.

Base Case

The base case serves as the termination condition for a recursive function. It defines the point at which the recursion stops and the function starts returning values. In a recursion tree, the nodes representing the base case are usually depicted as leaf nodes, as they do not result in further recursive calls.

Recursive Calls

The child nodes in a recursion tree represent the recursive calls made within the function. Each child node corresponds to a separate recursive call, resulting in the creation of new sub problems. The values or parameters passed to these recursive calls may differ, leading to variations in the sub problems' characteristics.

Execution Flow:

Traversing a recursion tree provides insights into the execution flow of a recursive function. Starting from the initial call at the root node, we follow the branches to reach subsequent calls until we encounter the base case. As the base cases are reached, the recursive calls start to return, and their respective nodes in the tree are marked with the returned values. The traversal continues until the entire tree has been traversed.

Time Complexity Analysis

Recursion trees aid in analyzing the time complexity of recursive algorithms. By examining the structure of the tree, we can determine the number of recursive calls made and the work done at each level. This analysis helps in understanding the overall efficiency of the algorithm and identifying any potential inefficiencies or opportunities for optimization.

Introduction

• Think of a program that determines a number's factorial. This function takes a number N as an input and returns the factorial of N as a result. This function's pseudo-code will resemble,

• Recursion is exemplified by the function that was previously mentioned. We are invoking a function to determine a number's factorial. Then, given a lesser value of the same number, this function calls itself. This continues until we reach the basic case, in which there are no more function calls.
• Recursion is a technique for handling complicated issues when the outcome is dependent on the outcomes of smaller instances of the same issue.
• If we think about functions, a function is said to be recursive if it keeps calling itself until it reaches the base case.
• Any recursive function has two primary components: the base case and the recursive step. We stop going to the recursive phase once we reach the basic case. To prevent endless recursion, base cases must be properly defined and are crucial. The definition of infinite recursion is a recursion that never reaches the base case. If a program never reaches the base case, stack overflow will continue to occur.

Recursion Types

Generally speaking, there are two different forms of recursion:

• Linear Recursion
• Tree Recursion
• Linear Recursion

Linear Recursion

• A function that calls itself just once each time it executes is said to be linearly recursive. A nice illustration of linear recursion is the factorial function. The name "linear recursion" refers to the fact that a linearly recursive function takes a linear amount of time to execute.
• Take a look at the pseudo-code below:

• If we look at the function doSomething(n), it accepts a parameter named n and does some calculations before calling the same procedure once more but with lower values.
• When the method doSomething() is called with the argument value n, let's say that T(n) represents the total amount of time needed to complete the computation. For this, we can also formulate a recurrence relation, T(n) = T(n-1) + K. K serves as a constant here. Constant K is included because it takes time for the function to allocate or de-allocate memory to a variable or perform a mathematical operation. We use K to define the time since it is so minute and insignificant.
• This recursive program's time complexity may be simply calculated since, in the worst scenario, the method doSomething() is called n times. Formally speaking, the function's temporal complexity is O(N).

Tree Recursion

• When you make a recursive call in your recursive case more than once, it is referred to as tree recursion. An effective illustration of Tree recursion is the fibonacci sequence. Tree recursive functions operate in exponential time; they are not linear in their temporal complexity.
• Take a look at the pseudo-code below,

• The only difference between this code and the previous one is that this one makes one more call to the same function with a lower value of n.
• Let's put T(n) = T(n-1) + T(n-2) + k as the recurrence relation for this function. K serves as a constant once more.
• When more than one call to the same function with smaller values is performed, this sort of recursion is known as tree recursion. The intriguing aspect is now: how time-consuming is this function?
• Take a guess based on the recursion tree below for the same function.
  
• It may occur to you that it is challenging to estimate the time complexity by looking directly at a recursive function, particularly when it is a tree recursion. Recursion Tree Method is one of several techniques for calculating the temporal complexity of such functions. Let's examine it in further detail.

What Is Recursion Tree Method?

• Recurrence relations like T(N) = T(N/2) + N or the two we covered earlier in the kinds of recursion section are solved using the recursion tree approach. These recurrence relations often use a divide and conquer strategy to address problems.
• It takes time to integrate the answers to the smaller sub problems that are created when a larger problem is broken down into smaller sub problems.
• The recurrence relation, for instance, is T(N) = 2 * T(N/2) + O(N) for the Merge sort. The time needed to combine the answers to two sub problems with a combined size of T(N/2) is O(N), which is true at the implementation level as well.
• For instance, since the recurrence relation for binary search is T(N) = T(N/2) + 1, we know that each iteration of binary search results in a search space that is cut in half. Once the outcome is determined, we exit the function. The recurrence relation has +1 added because this is a constant time operation.
• The recurrence relation T(n) = 2T(n/2) + Kn is one to consider. Kn denotes the amount of time required to combine the answers to n/2-dimensional sub problems.
• Let's depict the recursion tree for the aforementioned recurrence relation.

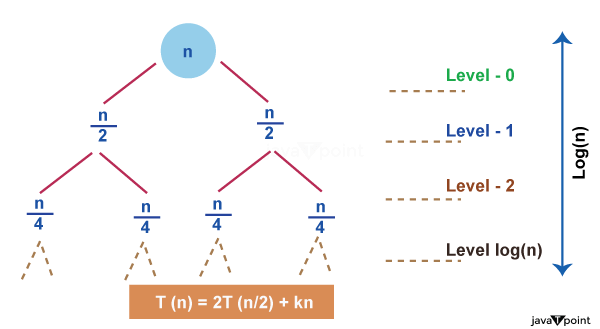
We may draw a few conclusions from studying the recursion tree above, including

1. The magnitude of the problem at each level is all that matters for determining the value of a node. The issue size is n at level 0, n/2 at level 1, n/2 at level 2, and so on.

2. In general, we define the height of the tree as equal to log (n), where n is the size of the issue, and the height of this recursion tree is equal to the number of levels in the tree. This is true because, as we just established, the divide-and-conquer strategy is used by recurrence relations to solve problems, and getting from issue size n to problem size 1 simply requires taking log (n) steps.

• Consider the value of N = 16, for instance. If we are permitted to divide N by 2 at each step, how many steps are required to get N = 1? Considering that we are dividing by two at each step, the correct answer is 4, which is the value of log(16) base 2.

log(16) base 2

log(2^4) base 2

4 * log(2) base 2, since log(a) base a = 1

so, 4 * log(2) base 2 = 4

3. At each level, the second term in the recurrence is regarded as the root.

Although the word "tree" appears in the name of this strategy, you don't need to be an expert on trees to comprehend it.

How to Use a Recursion Tree to Solve Recurrence Relations?

The cost of the sub problem in the recursion tree technique is the amount of time needed to solve the sub problem. Therefore, if you notice the phrase "cost" linked with the recursion tree, it simply refers to the amount of time needed to solve a certain sub problem.

Let's understand all of these steps with a few examples.

Example

Consider the recurrence relation,

T(n) = 2T(n/2) + K

Solution

The given recurrence relation shows the following properties,

A problem size n is divided into two sub-problems each of size n/2. The cost of combining the solutions to these sub-problems is K.

Each problem size of n/2 is divided into two sub-problems each of size n/4 and so on.

At the last level, the sub-problem size will be reduced to 1. In other words, we finally hit the base case.

Let's follow the steps to solve this recurrence relation,

Step 1: Draw the Recursion Tree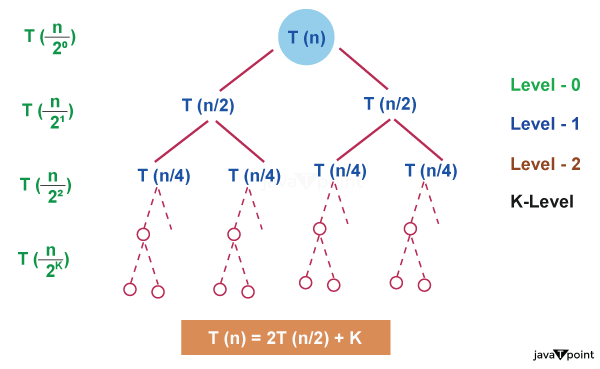

Step 2: Calculate the Height of the Tree

Since we know that when we continuously divide a number by 2, there comes a time when this number is reduced to 1. Same as with the problem size N, suppose after K divisions by 2, N becomes equal to 1, which implies, (n / 2^k) = 1

Here n / 2^k is the problem size at the last level and it is always equal to 1.

Now we can easily calculate the value of k from the above expression by taking log() to both sides. Below is a more clear derivation,

n = 2^k

• log(n) = log(2^k)
• log(n) = k * log(2)
• k = log(n) / log(2)
• k = log(n) base 2

So the height of the tree is log (n) base 2.

Step 3: Calculate the cost at each level

• Cost at Level-0 = K, two sub-problems are merged.
• Cost at Level-1 = K + K = 2*K, two sub-problems are merged two times.
• Cost at Level-2 = K + K + K + K = 4*K, two sub-problems are merged four times. and so on....

Step 4: Calculate the number of nodes at each level

Let's first determine the number of nodes in the last level. From the recursion tree, we can deduce this

• Level-0 have 1 (2^0) node
• Level-1 have 2 (2^1) nodes
• Level-2 have 4 (2^2) nodes
• Level-3 have 8 (2^3) nodes

So the level log(n) should have 2^(log(n)) nodes i.e. n nodes.

Step 5: Sum up the cost of all the levels

• The total cost can be written as,
• Total Cost = Cost of all levels except last level + Cost of last level
• Total Cost = Cost for level-0 + Cost for level-1 + Cost for level-2 +.... + Cost for level-log(n) + Cost for last level

The cost of the last level is calculated separately because it is the base case and no merging is done at the last level so, the cost to solve a single problem at this level is some constant value. Let's take it as O (1).

Let's put the values into the formulae,

• T(n) = K + 2*K + 4*K + .... + log(n)` times + `O(1) * n
• T(n) = K(1 + 2 + 4 + .... + log(n) times)` + `O(n)
• T(n) = K(2^0 + 2^1 + 2^2 + ....+ log(n) times + O(n)

If you closely take a look to the above expression, it forms a Geometric progression (a, ar, ar^2, ar^3 ...... infinite time). The sum of GP is given by S(N) = a / (r - 1). Here is the first term and r is the common ratio.