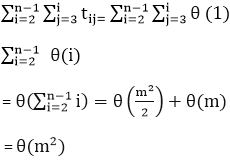Analyzing Algorithm Control StructureTo analyze a programming code or algorithm, we must notice that each instruction affects the overall performance of the algorithm and therefore, each instruction must be analyzed separately to analyze overall performance. However, there are some algorithm control structures which are present in each programming code and have a specific asymptotic analysis. Some Algorithm Control Structures are:
1. Sequencing:Suppose our algorithm consists of two parts A and B. A takes time tA and B takes time tB for computation. The total computation "tA + tB" is according to the sequence rule. According to maximum rule, this computation time is (max (tA,tB)). Example: Suppose tA =O (n) and tB = θ (n2). Then, the total computation time can be calculated as 2. If-then-else: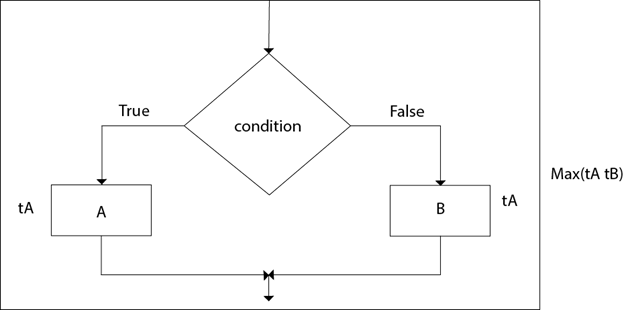
The total time computation is according to the condition rule-"if-then-else." According to the maximum rule, this computation time is max (tA,tB). Example: Suppose tA = O (n2) and tB = θ (n2) Calculate the total computation time for the following: 3. For loop:The general format of for loop is: Complexity of for loop:The outer loop executes N times. Every time the outer loop executes, the inner loop executes M times. As a result, the statements in the inner loop execute a total of N * M times. Thus, the total complexity for the two loops is O (N2) Consider the following loop: If the computation time ti for ( PI) various as a function of "i", then the total computation time for the loop is given not by a multiplication but by a sum i.e. Takes If the algorithms consist of nested "for" loops, then the total computation time is
For i ← 1 to n
{
For j ← 1 to n Example: Consider the following "for" loop, Calculate the total computation time for the following: Solution: The total Computation time is:
4. While loop:The Simple technique for analyzing the loop is to determine the function of variable involved whose value decreases each time around. Secondly, for terminating the loop, it is necessary that value must be a positive integer. By keeping track of how many times the value of function decreases, one can obtain the number of repetition of the loop. The other approach for analyzing "while" loop is to treat them as recursive algorithms. Algorithm:Example: The running time of algorithm array Max of computing the maximum element in an array of n integer is O (n). Solution: The number of primitive operation t (n) executed by this algorithm is at least. The best case T(n) =5n occurs when A [0] is the maximum element. The worst case T(n) = 7n-2 occurs when element are sorted in increasing order. We may, therefore, apply the big-Oh definition with c=7 and n0=1 and conclude the running time of this is O (n).
Next TopicRecurrence Relation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





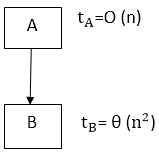 Computation Time = tA + tB
= (max (tA,tB)
= (max (O (n), θ (n2)) = θ (n2)
Computation Time = tA + tB
= (max (tA,tB)
= (max (O (n), θ (n2)) = θ (n2)
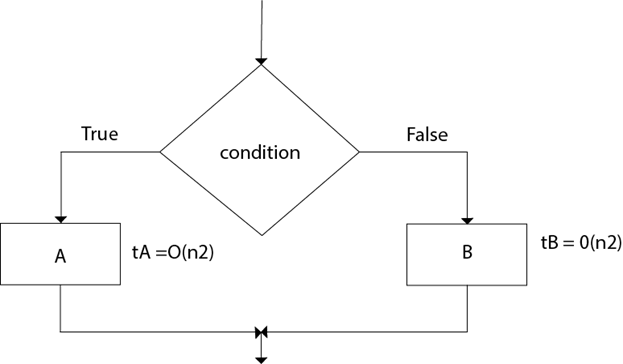 Total Computation = (max (tA,tB))
= max (O (n2), θ (n2) = θ (n2)
Total Computation = (max (tA,tB))
= max (O (n2), θ (n2) = θ (n2)
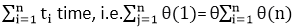
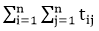 {
P (ij)
}
}
{
P (ij)
}
}