Maximum Sum Increasing Subsequence

The maximum sum increasing subsequence is a subsequence of a list of integers where the sum is maximum and, in a subsequence, all the elements are sorted in increasing order.

For example:
Consider the array of a given integers:
A[] = {3, 2, 6, 4, 5, 1}

Output

Maximum sum increasing subsequence is {3, 4, 5}

Let's consider one more example to understand it clearly.

Consider an array which is given below:

Array: 4, 6, 1, 3, 8, 4, 6

Here, we consider three arrays; the first array stores the array values, the second array stores the maximum value, and the third array stores the actual sequence.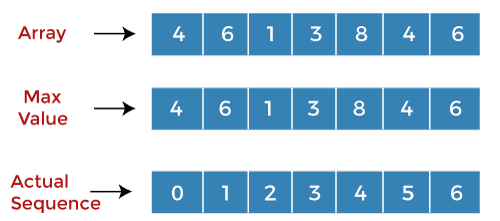

Initially, the second array stores the values of the array which is given in the problem and the third array stores the index corresponding to each value shown as below:

Assume two variables, 'i' and 'j'. For every 'i', 'j' will run till the 'i-1'. Compare the value at 'i' with a value at 'j'.

When i=0, j=0

A[i]=4

A[j] = 4

Since the values at 'i' and 'j' are the same, we will increment the value of 'i' and the value of 'i' becomes 1.

When i=1, j =0

A[i] = 6

A[j] = 4

Since A[i] > A[j] so we will add the values at 'i' and 'j', i.e., (6+4) equals to 10. We will replace the value 6 by 10 at i=1 in the second array. The value 1 is replaced by 0 at index i=1 in the third array and the value of 'i' is incremented shown as below: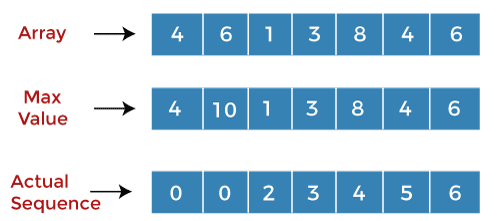

When i=2, j=0

A[i] = 1

A[j] = 4

Since A[i]<A[j] so there will be no addition, and the value of 'j' gets incremented. The value of 'j' becomes 1.

When i=2, j=1

A[i] = 1

A[j] = 6

Since A[j] > A[i] so there will be no addition, and the value of 'i' gets incremented. The value of 'i' becomes 3, and the value of 'j' is set to 0.

When i=3, j=0

A[3] = 3

A[0] = 4

Since A[j] > A[i] so there will be no addition, and the value of 'j' gets incremented. The value of 'j' becomes 1.

When i=3, j=1

A[3] = 3

A[1] = 6

Since A[i]<A[j] so there will be no addition, and the value of 'j' gets incremented. The value of 'j' becomes 2.

When i=3, j=2

A[3] = 3

A[2] = 1

Since A[i] > A[j] so we will add the values at 'i' and 'j', i.e., (3+1) equals to 4. We will replace the value 3 by 4 at i=3 in the second array. The value 3 is replaced by 2 at index i=3 in the third array and the value of 'i' is incremented shown as below: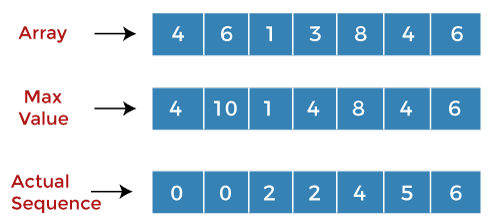

When i=4, j=0

A[4] = 8

A[j] = 4

Since A[i] > A[j], so we will add the values at 'i' and 'j', i.e., (8+4) equals to 12. We will replace the value 8 by 12 at i=4 in the second array. The value 4 is replaced by 0 at index i=4 in the third array, and the value of 'j' is incremented shown as below: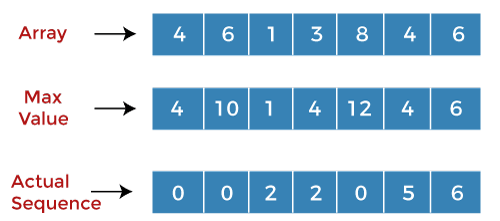

When i=4, j=1

A[4] = 8

A[1] = 6

Since A[i] > A[j] so we will add the values at 'i' and 'j'. The value corresponding to j in the second array is 10 so we will add (8+10) equals to 18. Since 18>12, so 12 will be replaced by 18 in the second array. The value 0 is replaced by 1 at the index 4 in the third array shown as below: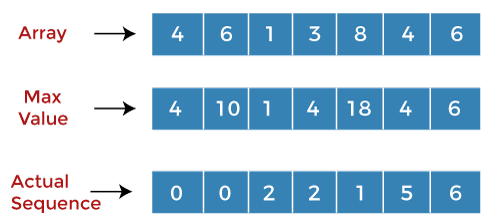

When i=4, j=2

A[4] = 8

A[2] = 1

Since A[i]>A[j] so we will add the values at 'i' and 'j'. The value corresponding to 'j' in the second array is 1, so we will add (8+1) equals to 9. The value 9 is less than the value 18, so there will be no replacement.

When i=4, j=3

A[4] = 8

A[3] = 3

Since A[i]>A[j] so we will add the values at 'i' and 'j'. The value corresponding to 'j' in the second array is 4 so we will add (8+4) equals to 12. The value 12 is less than the value 18 so there will be no replacement. The value of 'i' gets incremented.

When i=5, j=0

A[5] = 4

A[0] = 4

Since the value at 'j' is not less than the value at 'i' so we will increment the value of 'j'.

When i=5, j=1

A[5] = 4

A[1] = 6

Since A[i] is less than A[j] so the value of 'j' will be incremented.

When i=5, j=2

A[5] = 4

A[2] = 1

Since A[i]>A[j] so we will add the values at 'i' and 'j'. The value corresponding to 'j' in the second array is 1, so we will add (1+4) equals to 5. The value 5 is greater than the value 4, so 4 will be replaced by 5 at index 5 in the second array. The value 5 is replaced by 2 at index 5 in the third array shown as below: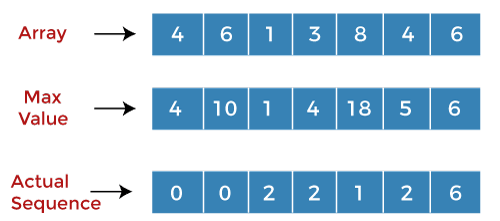

When i=5, j=3

A[5] = 4

A[3] = 3

Since A[i] >A[j] so we will add the values at 'i' and 'j'. The value corresponding to 'j' in the second array is 4, so we will add (4+4) equals to 8. The value 8 is greater than the value 5 so 5 will be replaced by 8 at index 5 in the second array. The value 2 is replaced by 3 at index 5 in the third array.

When i=5, j=4

A[5] = 4

A[4] = 8

Since A[j] > A[i] so the value of 'i' gets incremented. The value of 'i' becomes 6 and 'j' is set to 0.

When i=6, j=0

A[6] = 6

A[0] = 4

Since A[i] >A[j] so we will add the values at 'i' and 'j'. The value corresponding to 'j' in the second array is 4, so we will add (4+6) equals 10. The value 10 is greater than the value 6, so 6 will be replaced by 10 at index 6 in the second array. The value 6 is replaced by 0 at index 6 in the third array.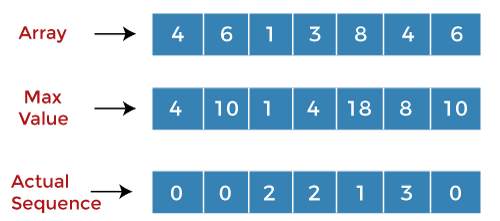

When i=6, j=1

A[6] = 6

A[1] = 6

Since A[6] == A[1] so the value of 'j' gets incremented. The value of 'j' equals to 2.

When i=6, j=2

A[6] = 6

A[2] = 1

Since A[i] >A[j] so we will add the values at 'i' and 'j'. The value corresponding to 'j' in the second array is 1, so we will add (1+6) equals 7. The value 7 is less than the value 10, so there will be no replacement.

When i=6, j=3

A[6] = 6

A[3] = 3

Since A[i] >A[j], so we will add the values at 'i' and 'j'. The value corresponding to 'j' in the second array is 4, so we will add (4+6) equals 10. The calculated value is the same as the value at index 6 in the second array.

When i=6, j=4

A[6] = 6

A[4] = 8

Since A[j] > A[i] so there will be no replacement. The value of 'j' gets incremented and becomes 5.

When i=6, j=5

A[6] = 6

A[5] = 4

Since A[i] >A[j] so we will add the values at 'i' and 'j'. The value corresponding to 'j' in the second array is 8, so we will add (8+6) equals 14. The value 14 is greater than the value 10, so 10 will be replaced by 14 at index 6 in the second array. The value 0 is replaced by 5 at index 6 in the third array shown as below: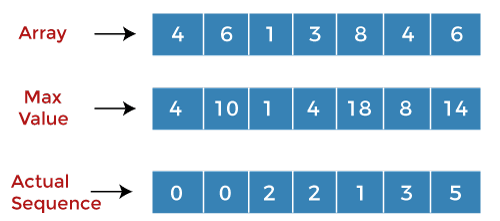

As we can observe in the maximum value array that 18 is the maximum sum of increasing subsequence. Now we will find the elements in the subsequence that forms 18 as the sum.

The element corresponding to the 18 is 8; therefore, the first element in the subsequence is 8.

Subsequence: 8

The value corresponding to 18 in the actual sequence array is 1. The value at index 1 is 6. Therefore, the second element in the subsequence is 6.

Subsequence: 6, 8

Move to index 1 in the actual sequence array. The value at index 1 is 0. The value at index 0 in an array is 4. So, the third element in the subsequence is 4.

Subsequence: 4, 6, 8

Implementation in C

// Program to calculate the maximum sum increasing subsequence 
#include <stdio.h>
// maximum_sum returns the maximum sum of increasing subsequence
int maximum_sum(int a[], int n)
{
    int i, j;
    int maximum_sum[n];
    int max=0;
    // Initializing the maximum_sum[] values for all the indexes 
    for (int i=0; i<n ; i++)
    {
        maximum_sum[i] = a[i];
    }    
    // Computing the values for all the indexes of maximum_sum[]
    for(int i=0; i<n; i++)
    {
        for(int j=0; j<i; j++)
        {
            if((a[i]>a[j]) && (maximum_sum[i]< (maximum_sum[j]+a[i]) ))
            {
                maximum_sum[i] = maximum_sum[j] + a[i];
            }
        }
    }
 // Calculating the maximum element from the maximum_sum[] array
    for(int i = 0; i<n; i++)
    {        
        //printf("%d,", maximum_sum[i]);
        if(max < maximum_sum[i])
        {
            max = maximum_sum[i];
        }
    }
 return max;
}
// main() method
int main()
{
  int arr[5] = {1, 5, 6, 4, 3}; // array initialization
  int size = sizeof(arr)/sizeof(arr[0]);

  printf("Maximum sum of increasing subsequence is : %d", maximum_sum(arr, size));
  return 0;
}

Output