NP-CompletenessA decision problem L is NP-Hard if L' ≤p L for all L' ϵ NP. Definition: L is NP-complete if
P: is the set of decision problems that are solvable in polynomial time. NP: is the set of decision problems that can be verified in polynomial time. NP-Hard: L is NP-hard if for all L' ϵ NP, L' ≤p L. Thus if we can solve L in polynomial time, we can solve all NP problems in polynomial time. NP-Complete L is NP-complete if
If any NP-complete problem is solvable in polynomial time, then every NP-Complete problem is also solvable in polynomial time. Conversely, if we can prove that any NP-Complete problem cannot be solved in polynomial time, every NP-Complete problem cannot be solvable in polynomial time. ReductionsConcept: - If the solution of NPC problem does not exist then the conversion from one NPC problem to another NPC problem within the polynomial time. For this, you need the concept of reduction. If a solution of the one NPC problem exists within the polynomial time, then the rest of the problem can also give the solution in polynomial time (but it's hard to believe). For this, you need the concept of reduction. Example: - Suppose there are two problems, A and B. You know that it is impossible to solve problem A in polynomial time. You want to prove that B cannot be solved in polynomial time. So you can convert the problem A into problem B in polynomial time. Example of NP-Complete problemNP problem: - Suppose a DECISION-BASED problem is provided in which a set of inputs/high inputs you can get high output. Criteria to come either in NP-hard or NP-complete.
Note1:- If you satisfy both points then your problem comes into the category of NP-complete classNote2:- If you satisfy the only 2nd points then your problem comes into the category of NP-hard classSo according to the given decision-based NP problem, you can decide in the form of yes or no. If, yes then you have to do verify and convert into another problem via reduction concept. If you are being performed, both then decision-based NP problems are in NP compete. Here we will emphasize NPC. 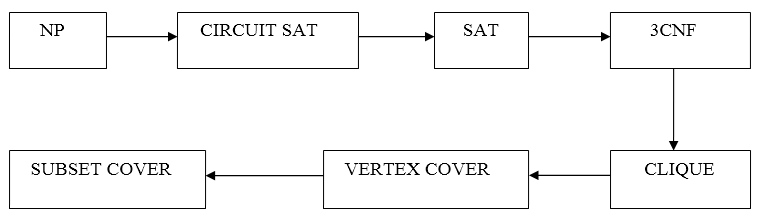
Next TopicCircuit Satisfiability
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










