Optimal Substructure PropertyA given optimal substructure property if the optimal solution of the given problem can be obtained by finding the optimal solutions of all the sub-problems. In other words, we can solve larger problems given the solution of smaller problems. Suppose we have given a complex problem, then we will break this problem into simpler problems optimally to find the optimal solution of the given complex problem. For example: f(n) = f(n-1) + f(n-2) 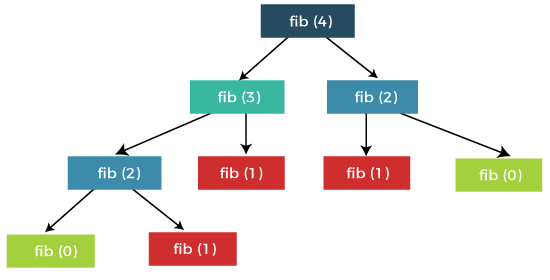
In the above example, the problem f(n) is broken into two smaller problems, i.e., F(n-1) and f(n-2). These two smaller problems can also be broken further into smaller problems. The above figure shows how problems are broken down into the sub-problems. This process will continue till the problem cannot be further divided. Once the sub-problem is not further divided, we will take the base cases to find the solution. Principle of Optimality Richard Bellman was a scientist who worked on dynamic programming in 1957. Let's understand the optimality through an example. 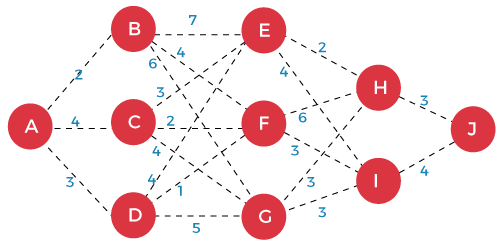
Let F(x) be the minimum distance required to reach J from a node X. Assume that F(J) =0. The distance from the vertex H to the vertex J is 3, and the distance from vertex I to vertex J is 4. Now we calculate the distance from the vertex E to vertex J is given below: F(E) = min{ 1+F(H), 4+F(I)} =min{4, 8} The minimum value is 4; therefore, the distance from vertex E to vertex J would be 4. Now we calculate the distance from the vertex F to vertex J is given below: F(F) = min{ 6+F(H), 3+F(I)} = min{9, 7} The minimum value is 7; therefore, the distance from vertex F to vertex J would be 7. Now we calculate the distance from the vertex G to vertex J is given below: F(G) = min{ 3+F(H), 3+F(I)} = min{6, 7} The minimum value is 6; therefore, the distance from vertex G to vertex J would be 6. Now we calculate the distance from the vertex B to vertex J is given below: F(B) = min{ 7+F(E), 4+F(F), 6+F(G)} = min{11, 11, 12} The minimum value is 11; therefore, the distance from vertex B to vertex J would be 11. Now we calculate the distance from the vertex C to vertex J is given below: F(C) = min{ 3+F(E), 2+F(F), 4+F(G)} = min{6, 4, 8} The minimum value is 4; therefore, the distance from vertex C to vertex J would be 11. Now we calculate the distance from the vertex D to vertex J is given below: F(D) = min{ 4+F(E), 1+F(F), 5+F(G)} = min{8, 8, 11} The minimum value is 8; therefore, the distance from vertex D to vertex J would be 8. Now we calculate the distance from the vertex A to vertex J is given below: F(A) = min{ 2+F(B), 4+F(C), 3+F(D)} = min{13, 11, 11} The minimum value is 11; therefore, the distance from vertex A to vertex J would be 11. Therefore, we can say that the minimum distance from A to J is 11. Now, we have two ways to reach from the vertex A to J through vertex D:
Here, we have built an optimal solution using the sub-solutions to the problem. Therefore, we can say that the above problem has an optimal substructure. We can prove the above problem by using the proof by contradiction. Let Ra...j be the optimal path from the nodes A to J. Let's assume that this optimal path takes to the destination through node k. Now, the path can be split into Ra..k and Rk...J Let's understand through the diagrammatic representation. Assume that there is a shorter path from A to K and name it as R`a..k if R`a..k < Ra..k then R`a..k + Rk..j < Ra..k + Rk..j The above relation cannot be true as we already know that Ra..k + Rk..j is an optimal solution, as stated before. Therefore, R`a..k, a shorter path from a to k does not exist, and Ra..k + Rk..j is indeed the optimal solution. Problems without Optimal SubstructureTwo problems can occur without an Optimal substructure:
Let's look at the longest path problem first. Consider the below graph having 5 vertices. 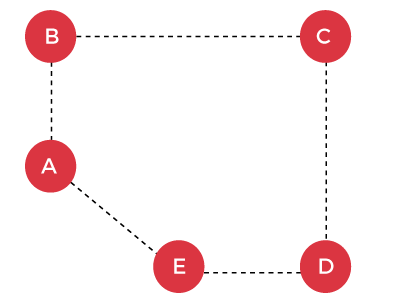
The goal of the problem is to find the longest path between two vertices without repeating an edge. Suppose we want to find the longest path from A to C, i.e., LongestPath(A, C). There are two ways to travel from A to C:
The first way provides the solution for the longest path, as the second way does not provide the longest path. The principle of optimality is shown below: The above figure depicts the path from A to B and then B to C, and this is the optimal solution. But the optimal path is not the solution of the longest path. If the principle of optimality applies to the Longest Path problem, then we should split up the problem into sub-parts. The longest-path from A to C can be written as: Longestpath(A, C) = Longest_path(A, D) + (D-C) There are two possible ways of finding the longest path from A to D:
The second way provides the longest path. If we add this path to the edge (D-C), there would be a repeating edge, i.e., D to C which is not allowed. So, in this case, the sub-solutions of a problem do not combine to form the overall optimal solution. Therefore, we can say that the Longest-path problem does not exhibit an Optimal substructure. Maximum Clique Problem Here, Clique means that all the vertices are attached to each other. The maximum clique means with the most vertices in a graph. Let's understand the maximum clique through an example. Consider the below graph: 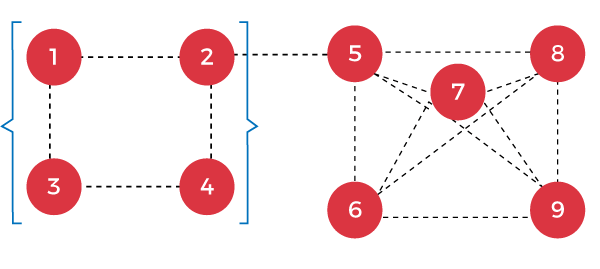
Vertices: {1, 2, 3, 4, 5, 6, 7, 8, 9} Maximum clique: {5, 6, ,7, 8, 9} If principle of optimality applies to Maximum clique Problem, then we should split up the problem into sub-parts: Vertices = {1, 2, 3, 4, 5, 6, 7} + {8, 9} Maximal clique = {5, 6, 7, 8, 9} Cliques = {1, 2, 3, 4}, {5, 6, 7} + {8, 9}
Next TopicOverlapping sub-problems
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









