Single Source Shortest PathsIntroduction:In a shortest- paths problem, we are given a weighted, directed graphs G = (V, E), with weight function w: E → R mapping edges to real-valued weights. The weight of path p = (v0,v1,..... vk) is the total of the weights of its constituent edges: 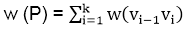
We define the shortest - path weight from u to v by δ(u,v) = min (w (p): u→v), if there is a path from u to v, and δ(u,v)= ∞, otherwise. The shortest path from vertex s to vertex t is then defined as any path p with weight w (p) = δ(s,t). The breadth-first- search algorithm is the shortest path algorithm that works on unweighted graphs, that is, graphs in which each edge can be considered to have unit weight. In a Single Source Shortest Paths Problem, we are given a Graph G = (V, E), we want to find the shortest path from a given source vertex s ∈ V to every vertex v ∈ V. Variants:There are some variants of the shortest path problem.
Shortest Path: Existence:If some path from s to v contains a negative cost cycle then, there does not exist the shortest path. Otherwise, there exists a shortest s - v that is simple. 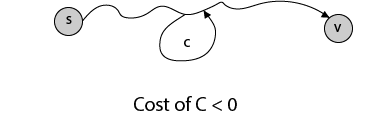
Next TopicNegative Weight Edges
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










