Example of Matrix Chain MultiplicationExample: We are given the sequence {4, 10, 3, 12, 20, and 7}. The matrices have size 4 x 10, 10 x 3, 3 x 12, 12 x 20, 20 x 7. We need to compute M [i,j], 0 ≤ i, j≤ 5. We know M [i, i] = 0 for all i. 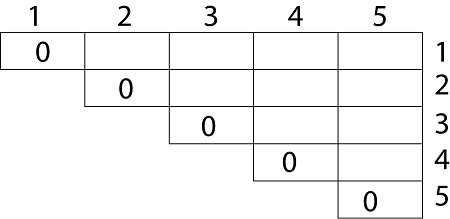
Let us proceed with working away from the diagonal. We compute the optimal solution for the product of 2 matrices. 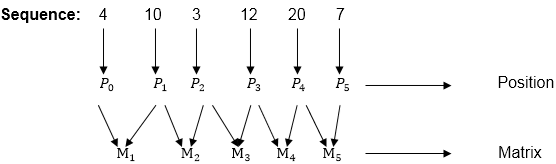
Here P0 to P5 are Position and M1 to M5 are matrix of size (pi to pi-1) On the basis of sequence, we make a formula 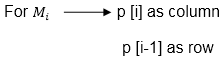
In Dynamic Programming, initialization of every method done by '0'.So we initialize it by '0'.It will sort out diagonally. We have to sort out all the combination but the minimum output combination is taken into consideration.
Calculation of Product of 2 matrices:
1. m (1,2) = m1 x m2
= 4 x 10 x 10 x 3
= 4 x 10 x 3 = 120
2. m (2, 3) = m2 x m3
= 10 x 3 x 3 x 12
= 10 x 3 x 12 = 360
3. m (3, 4) = m3 x m4
= 3 x 12 x 12 x 20
= 3 x 12 x 20 = 720
4. m (4,5) = m4 x m5
= 12 x 20 x 20 x 7
= 12 x 20 x 7 = 1680
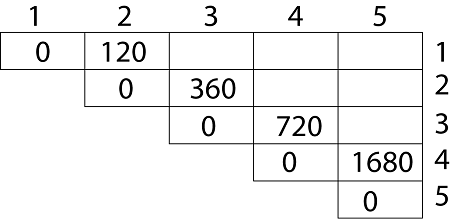
Now the third diagonal will be solved out in the same way. Now product of 3 matrices: M [1, 3] = M1 M2 M3
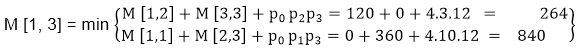
M [1, 3] =264 As Comparing both output 264 is minimum in both cases so we insert 264 in table and ( M1 x M2) + M3 this combination is chosen for the output making. M [2, 4] = M2 M3 M4
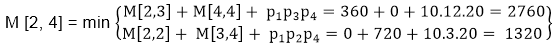
M [2, 4] = 1320 As Comparing both output 1320 is minimum in both cases so we insert 1320 in table and M2+(M3 x M4) this combination is chosen for the output making. M [3, 5] = M3 M4 M5
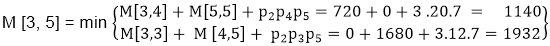
M [3, 5] = 1140 As Comparing both output 1140 is minimum in both cases so we insert 1140 in table and ( M3 x M4) + M5this combination is chosen for the output making. 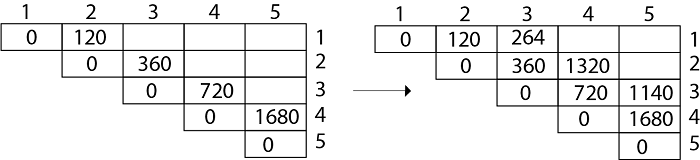
Now Product of 4 matrices: M [1, 4] = M1 M2 M3 M4 There are three cases by which we can solve this multiplication:
After solving these cases we choose the case in which minimum output is there 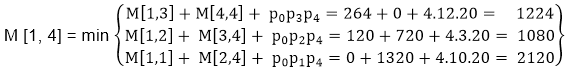
M [1, 4] =1080 As comparing the output of different cases then '1080' is minimum output, so we insert 1080 in the table and (M1 xM2) x (M3 x M4) combination is taken out in output making, M [2, 5] = M2 M3 M4 M5 There are three cases by which we can solve this multiplication:
After solving these cases we choose the case in which minimum output is there 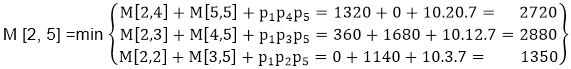
M [2, 5] = 1350 As comparing the output of different cases then '1350' is minimum output, so we insert 1350 in the table and M2 x( M3 x M4 xM5)combination is taken out in output making. 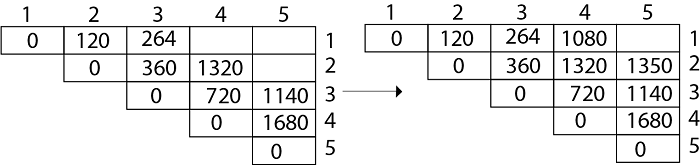
Now Product of 5 matrices: M [1, 5] = M1 M2 M3 M4 M5 There are five cases by which we can solve this multiplication:
After solving these cases we choose the case in which minimum output is there 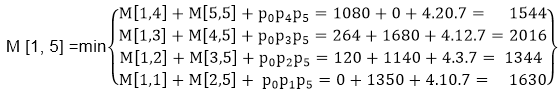
M [1, 5] = 1344 As comparing the output of different cases then '1344' is minimum output, so we insert 1344 in the table and M1 x M2 x(M3 x M4 x M5)combination is taken out in output making. Final Output is: 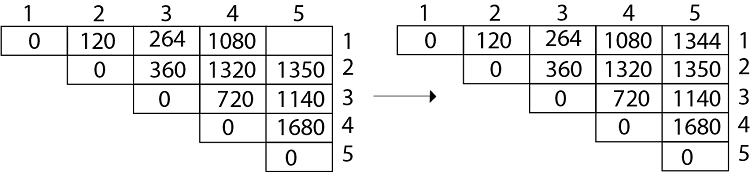
Step 3: Computing Optimal Costs: let us assume that matrix Ai has dimension pi-1x pi for i=1, 2, 3....n. The input is a sequence (p0,p1,......pn) where length [p] = n+1. The procedure uses an auxiliary table m [1....n, 1.....n] for storing m [i, j] costs an auxiliary table s [1.....n, 1.....n] that record which index of k achieved the optimal costs in computing m [i, j]. The algorithm first computes m [i, j] ← 0 for i=1, 2, 3.....n, the minimum costs for the chain of length 1.
Next TopicMatrix Chain Multiplication Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










