Overlapping sub-problemsDynamic programming is an approach used to solve the complex problem by breaking down the problem into sub-problems and storing the results of the sub-problem to avoid the re-computation of the same sub-problem again and again. The following are the two properties of a problem that indicates that the given problem can be solved by using the dynamic programming approach:
We have already discussed the optimal substructure. Now we will discuss the overlapping subproblems. What is an overlapping sub-problem?Dynamic programming is used where the solutions of the same sub-problems are required again and again. It is similar to the divide and conquer approach, where the solution is computed by combining the solutions of all the sub-problems. Dynamic programming is used because the solutions of sub-problems can be stored in a table so that it does not need to recompute again and again. Dynamic programming is not required when there are no common or overlapping sub-problems as there is no use of storing the results in a table again and again. For example, Binary search does not require dynamic programming as it has no common sub-problems. In contrast, a recursive program of Fibonacci series has many common sub-problems, so it requires a dynamic programming approach to solve the problem optimally. Recursive program of Fibonacci series If we want to calculate fib(5), then the diagrammatic representation of f(5) is shown below: 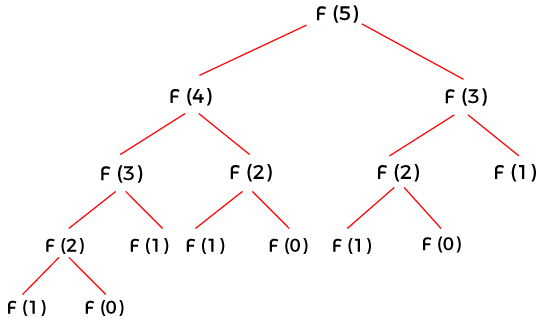
As we can observe in the above figure that the value of fib(3) is computed twice and the value of fib(2) is computed three times. Instead of computing the value again and again, we can store the computed value in a table so that we do not need to re-compute the value of sub-problem again and again. There are two ways that we can use to store the values:
What is Memoization?Memoization is a technique that stores the result of the sub-problem. Memoization technique is almost similar to the recursive technique with a small difference that memorization looks into the lookup table before computing the sub-problem. In the memorization technique, a lookup table is used. Initially, a look up table is initialized with NIL values. Whenever we require a solution of the sub-problem then we first look into the look up table and if we do not find the solution into the look up table then we compute the sub-problem and stores the result into the look up table so that it can be reused later. Program Explanation In the above code, we have declared a MAX variable using #define directive. The value 50 is assigned to the MAX variable. The lookup is an array of type int having MAX size. Initially, we have assigned -1 value to the lookup array. The function fib(n) is created to find the Fibonacci number of n. In this function, we will check whether the value of lookup[n] is equal to -1 or not. If the value of n is less than or equal to -1 then the value of lookup[n] is equal to n; otherwise, it will contain the summation of the solutions of two sub-problems, i.e., fib(n-1) + fib(n-2). Output 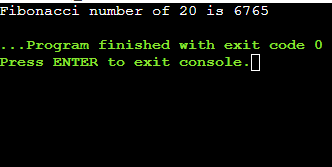
What is Tabulation?In the tabulation technique, we solve the sub-problems in a bottom-up fashion and use the solutions of sub-problems to reach at the bigger sub-problems. The tabulation technique can be used as generating the solutions of bigger sub-problems iteratively by using the solutions of the smaller sub-problems. Program Explanation In the above code, we have declared an array of size n+1. The base cases are f[0] and f[1] with the values, 0 and 1, respectively. We have found the solutions to all the bigger problems by using the solutions of all the smaller problems with the help of statement f[i] = f[i-1] + f[i-2]. Output 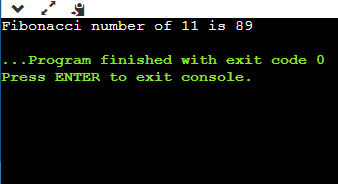
Both tabulation and memoization are used to store the solutions of sub-problems. In memoization, table entry is filled on demand; it means that its not mandatory that all the entries are completely filled. In the tabulation technique, all the table entries are filled one by one starting from the very first entry.
Next TopicDynamic programming vs Greedy approach
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









