Heap Sort

Binary Heap:

Binary Heap is an array object can be viewed as Complete Binary Tree. Each node of the Binary Tree corresponds to an element in an array.

1. Length [A],number of elements in array
2. Heap-Size[A], number of elements in a heap stored within array A.

The root of tree A [1] and gives index 'i' of a node that indices of its parents, left child, and the right child can be computed.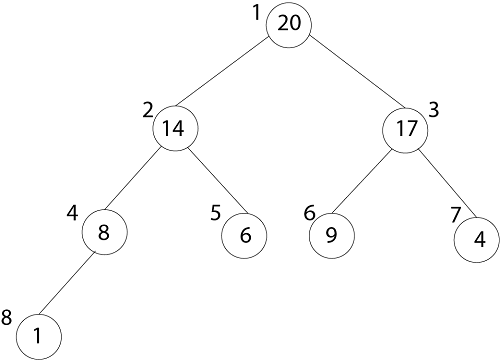

Representation of an array of the above figure is given below: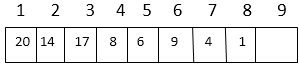

The index of 20 is 1

To find the index of the left child, we calculate 1*2=2

This takes us (correctly) to the 14.

Now, we go right, so we calculate 2*2+1=5

This takes us (again, correctly) to the 6.

Now, 4's index is 7, we want to go to the parent, so we calculate 7/2 =3 which takes us to the 17.

Heap Property:

A binary heap can be classified as Max Heap or Min Heap

1. Max Heap: In a Binary Heap, for every node I other than the root, the value of the node is greater than or equal to the value of its highest child

Thus, the highest element in a heap is stored at the root. Following is an example of MAX-HEAP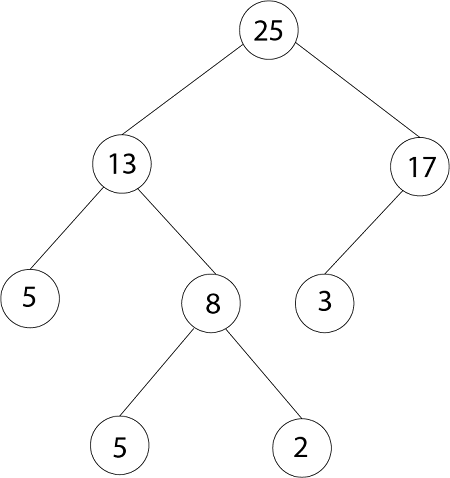

2. MIN-HEAP: In MIN-HEAP, the value of the node is lesser than or equal to the value of its lowest child.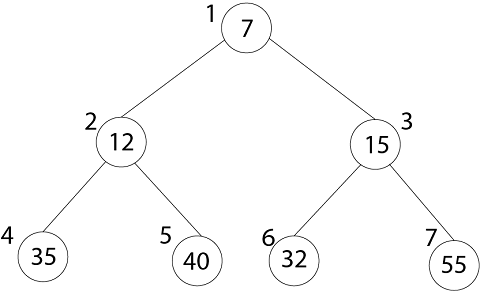

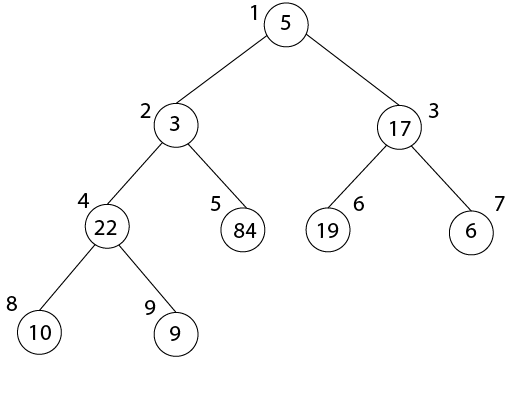
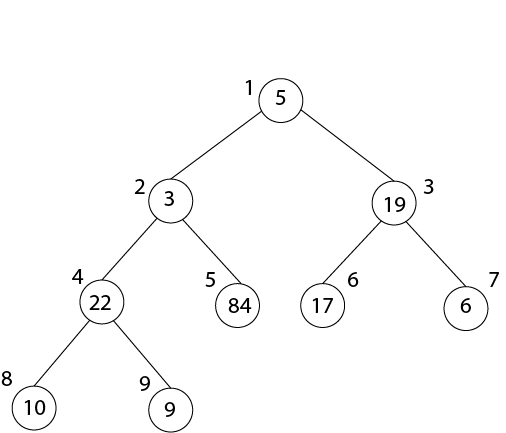
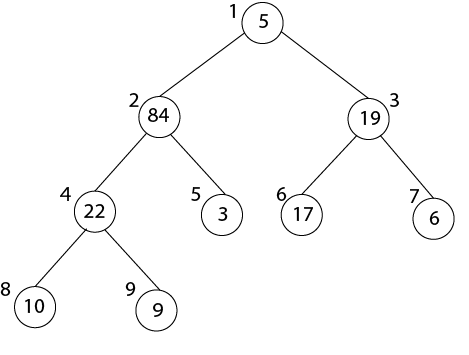
Heapify Method:

1. Maintaining the Heap Property: Heapify is a procedure for manipulating heap Data Structure. It is given an array A and index I into the array. The subtree rooted at the children of A [i] are heap but node A [i] itself may probably violate the heap property i.e. A [i] < A [2i] or A [2i+1]. The procedure 'Heapify' manipulates the tree rooted as A [i] so it becomes a heap.

MAX-HEAPIFY (A, i)
 1. l ← left [i]
 2. r ← right [i]
 3. if l≤ heap-size [A] and A[l] > A [i]
 4. then largest ← l
 5. Else largest ← i
 6. If r≤ heap-size [A] and A [r] > A[largest]
 7. Then largest ← r
 8. If largest ≠ i
 9. Then exchange A [i]    A [largest]
 10. MAX-HEAPIFY (A, largest)

Analysis:

The maximum levels an element could move up are Θ (log n) levels. At each level, we do simple comparison which O (1). The total time for heapify is thus O (log n).

Building a Heap:

BUILDHEAP (array A, int n)
 1 for i ← n/2 down to 1
 2 do
 3 HEAPIFY (A, i, n)

HEAP-SORT ALGORITHM:

HEAP-SORT (A)
 1. BUILD-MAX-HEAP (A)
 2. For I ← length[A] down to Z
 3. Do exchange A [1] ←→ A [i]
 4. Heap-size [A] ← heap-size [A]-1
 5. MAX-HEAPIFY (A,1)

Analysis: Build max-heap takes O (n) running time. The Heap Sort algorithm makes a call to 'Build Max-Heap' which we take O (n) time & each of the (n-1) calls to Max-heap to fix up a new heap. We know 'Max-Heapify' takes time O (log n)

The total running time of Heap-Sort is O (n log n).

Example: Illustrate the Operation of BUILD-MAX-HEAP on the array.

Solution: Originally: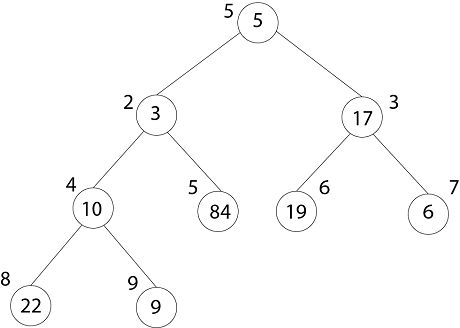

Priority Queue:

As with heaps, priority queues appear in two forms: max-priority queue and min-priority queue.

A priority queue is a data structure for maintaining a set S of elements, each with a combined value called a key. A max-priority queue guides the following operations:

INSERT(S, x): inserts the element x into the set S, which is proportionate to the operation S=S∪[x].

MAXIMUM (S) returns the element of S with the highest key.

EXTRACT-MAX (S) removes and returns the element of S with the highest key.

INCREASE-KEY(S, x, k) increases the value of element x's key to the new value k, which is considered to be at least as large as x's current key value.

Let us discuss how to implement the operations of a max-priority queue. The procedure HEAP-MAXIMUM consider the MAXIMUM operation in θ (1) time.

HEAP-MAXIMUM (A)

1. return A [1]

The procedure HEAP-EXTRACT-MAX implements the EXTRACT-MAX operation. It is similar to the for loop of Heap-Sort procedure.

HEAP-EXTRACT-MAX (A)
 1 if A. heap-size < 1
 2 error "heap underflow"
 3 max ← A [1]
 4 A [1] ← A [heap-size [A]]
 5 heap-size [A] ← heap-size [A]-1
 6 MAX-HEAPIFY (A, 1)
 7 return max

The procedure HEAP-INCREASE-KEY implements the INCREASE-KEY operation. An index i into the array identify the priority-queue element whose key we wish to increase.

HEAP-INCREASE-KEY.A, i, key)
 1 if key < A[i]
 2 errors "new key is smaller than current key"
 3 A[i] = key 
 4 while i>1 and A [Parent (i)] < A[i] 
 5 exchange A [i] with A [Parent (i)] 
 6 i =Parent [i]

The running time of HEAP-INCREASE-KEY on an n-element heap is O (log n) since the path traced from the node updated in line 3 to the root has length O (log n).

The procedure MAX-HEAP-INSERT implements the INSERT operation. It takes as an input the key of the new item to be inserted into max-heap A. The procedure first expands the max-heap by calculating to the tree a new leaf whose key is - ∞. Then it calls HEAP-INCREASE-KEY to set the key of this new node to its right value and maintain the max-heap property

MAX-HEAP-INSERT (A, key)
 1 A. heap-size = A. heap-size + 1 
 2 A [A. heap-size] = - ∞
 3 HEAP-INCREASE-KEY (A, A. heap-size, key)

The running time of MAX-HEAP-INSERT on an n-element heap is O (log n).

Example: Illustrate the operation of HEAP-EXTRACT-MAX on the heap

Fig: Operation of HEAP-INCREASE-KEY

Fig: (a)

In this figure, that max-heap with a node whose index is 'i' heavily shaded

Fig: (b)

In this Figure, this node has its key increased to 15.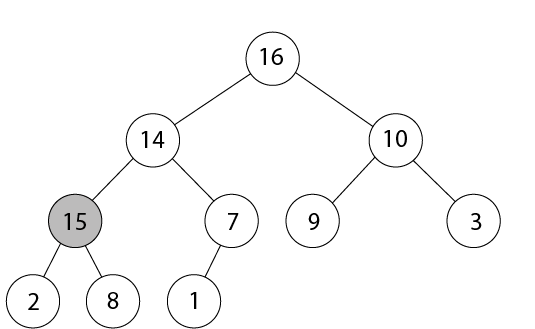

Fig: (c)

After one iteration of the while loop of lines 4-6, the node and its parent have exchanged keys, and the index i moves up to the parent.

Fig: (d)

The max-heap after one more iteration of the while loops, the A [PARENT (i) ≥A (i)] the max-heap property now holds and the procedure terminates.

Heap-Delete:

Heap-DELETE (A, i) is the procedure, which deletes the item in node 'i' from heap A, HEAP-DELETE runs in O (log n) time for n-element max heap.

HEAP-DELETE (A, i)
 1. A [i] ← A [heap-size [A]]
 2. Heap-size [A] ← heap-size [A]-1
 3. MAX-HEAPIFY (A, i)