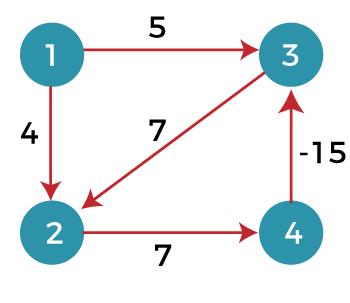
Bellman Ford Algorithm

Bellman ford algorithm is a single-source shortest path algorithm. This algorithm is used to find the shortest distance from the single vertex to all the other vertices of a weighted graph. There are various other algorithms used to find the shortest path like Dijkstra algorithm, etc. If the weighted graph contains the negative weight values, then the Dijkstra algorithm does not confirm whether it produces the correct answer or not. In contrast to Dijkstra algorithm, bellman ford algorithm guarantees the correct answer even if the weighted graph contains the negative weight values.

Rule of this algorithm

Consider the below graph: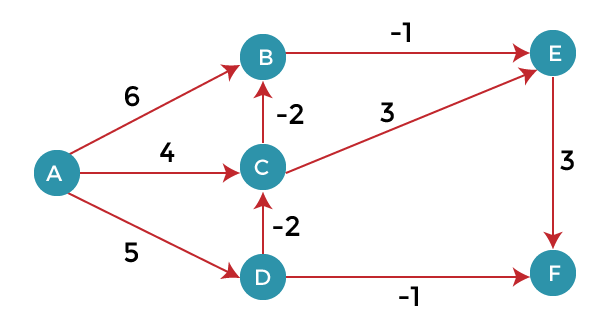

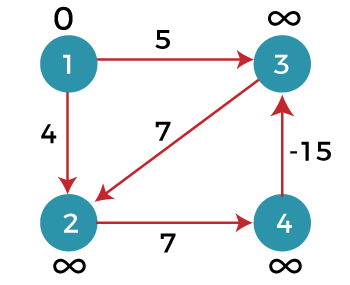
As we can observe in the above graph that some of the weights are negative. The above graph contains 6 vertices so we will go on relaxing till the 5 vertices. Here, we will relax all the edges 5 times. The loop will iterate 5 times to get the correct answer. If the loop is iterated more than 5 times then also the answer will be the same, i.e., there would be no change in the distance between the vertices.

Relaxing means:

To find the shortest path of the above graph, the first step is note down all the edges which are given below:

(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)

Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below: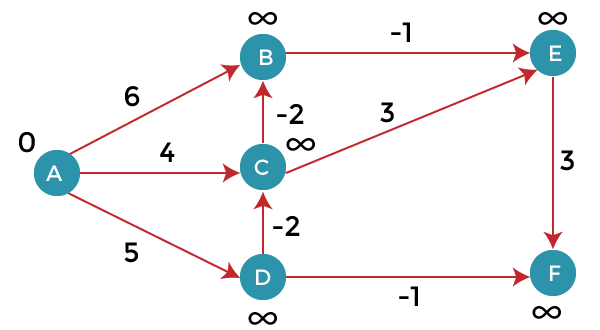

Since the graph has six vertices so it will have five iterations.

First iteration

Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:

d(u) = 0

d(v) = ∞

c(u , v) = 6

Since (0 + 6) is less than ∞, so update

d(v) = 0 + 6 = 6

Therefore, the distance of vertex B is 6.

Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:

d(u) = 0

d(v) = ∞

c(u , v) = 4

Since (0 + 4) is less than ∞, so update

d(v) = 0 + 4 = 4

Therefore, the distance of vertex C is 4.

Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:

d(u) = 0

d(v) = ∞

c(u , v) = 5

Since (0 + 5) is less than ∞, so update

d(v) = 0 + 5 = 5

Therefore, the distance of vertex D is 5.

Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:

d(u) = 6

d(v) = ∞

c(u , v) = -1

Since (6 - 1) is less than ∞, so update

d(v) = 6 - 1= 5

Therefore, the distance of vertex E is 5.

Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:

d(u) = 4

d(v) = 5

c(u , v) = 3

Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.

Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:

d(u) = 5

d(v) = 4

c(u , v) = -2

Since (5 -2) is less than 4, so update

d(v) = 5 - 2 = 3

Therefore, the distance of vertex C is 3.

Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:

d(u) = 5

d(v) = ∞

c(u , v) = -1

Since (5 -1) is less than ∞, so update

d(v) = 5 - 1 = 4

Therefore, the distance of vertex F is 4.

Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:

d(u) = 5

d(v) = ∞

c(u , v) = 3

Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.

Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:

d(u) = 3

d(v) = 6

c(u , v) = -2

Since (3 - 2) is less than 6, so update

d(v) = 3 - 2 = 1

Therefore, the distance of vertex B is 1.

Now the first iteration is completed. We move to the second iteration.

Second iteration:

In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.

The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.

The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.

The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:

d(v) = d(u) + c(u, v)

d(E) = d(B) +c(B , E)

= 1 - 1 = 0

The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.

The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.

The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.

The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.

The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.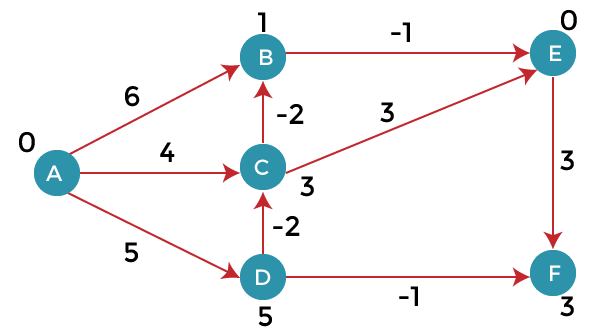

Third iteration

We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.

Time Complexity

The time complexity of Bellman ford algorithm would be O(E|V| - 1).

Drawbacks of Bellman ford algorithm

• The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph.
  
• In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below:
  
  Edges can be written as:
  (1, 3), (1, 2), (2, 4), (3, 2), (4, 3)

First iteration

Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:

d(u) = 0

d(v) = ∞

c(u , v) = 5

Since (0 + 5) is less than ∞, so update

d(v) = 0 + 5 = 5

Therefore, the distance of vertex 3 is 5.

Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:

d(u) = 0

d(v) = ∞

c(u , v) = 4

Since (0 + 4) is less than ∞, so update

d(v) = 0 + 4 = 4

Therefore, the distance of vertex 2 is 4.

Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:

d(u) = 5

d(v) = 4

c(u , v) = 7

Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.

Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:

d(u) = 4

d(v) = ∞

c(u , v) = 7

Since (4 + 7) equals to 11 which is less than ∞, so update

d(v) = 4 + 7 = 11

Therefore, the distance of vertex 4 is 11.

Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:

d(u) = 11

d(v) = 5

c(u , v) = -15

Since (11 - 15) equals to -4 which is less than 5, so update

d(v) = 11 - 15 = -4

Therefore, the distance of vertex 3 is -4.

Now we move to the second iteration.

Second iteration

Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.

The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.

The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:

d(v) = d(u) + c(u, v)

d(2) = d(3) +c(3, 2)

= -4 + 7 = 3

Therefore, the value at vertex 2 is 3.

The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update

d(v) = d(u) + c(u, v)

d(4) = d(2) +c(2, 4)

= 3 + 7 = 10

Therefore, the value at vertex 4 is 10.

The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:

d(v) = d(u) + c(u, v)

d(3) = d(4) +c(4, 3)

= 10 - 15 = -5

Therefore, the value at vertex 3 is -5.

Now we move to the third iteration.

Third iteration

Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.

The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.

The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:

d(v) = d(u) + c(u, v)

d(2) = d(3) +c(3, 2)

= -5 + 7 = 2

Therefore, the value at vertex 2 is 2.

The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:

d(v) = d(u) + c(u, v)

d(4) = d(2) +c(2, 4)

= 2 + 7 = 9

Therefore, the value at vertex 4 is 9.

The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:

d(v) = d(u) + c(u, v)

d(3) = d(4) +c(4, 3)

= 9 - 15 = -6

Therefore, the value at vertex 3 is -6.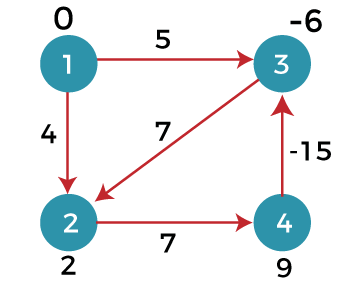

Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4^th iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.

4^th iteration

The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.

The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.

The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:

d(v) = d(u) + c(u, v)

d(2) = d(3) +c(3, 2)

= -6 + 7 = 1

In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.

Therefore, the value at vertex 2 is 1.